解の公式は分解と不変化から
このワークシートはMath by Codeの一部です。
2次方程式の解の公式を導くためには、平方完成をするのが普通です。
また、因数定理や多項式の係数分離の割り算(組み立て除法)などを使えば、
解の公式も平方完成も使わずに、次元下げができます。
数値方程式ならその方針はとても重要です。
でも、係数が数値ではない文字だけの一般方程式の解の公式を作るときは、
方針を変える必要があります。
一般方程式の解の公式を作る鍵は分解にある。
手始めに、2次方程式の解の公式を作ってみよう。
<2次方程式>
解の公式を作るための土台
・2次式で対称式×交代式に因数分解できるものがある。x2-y2=(x+y)(x-y)
・連立方程式 x+y=p, x-y=qからx=(p+q)/2、y=(p-q)/2
(ゴール地点)解の公式
モニック(最高次の係数が1)な2次方程式f(x)=x2-ax+b=0の解の公式は
x=(α,β)=(a±√D)/2 (D=a2-4b)
(スタート地点)ガロア理論
2次方程式のf(x)=x2-ax+b=0の基礎体をF=Qとして、f(x)の最小分解体をE=Q(α,β)とする。
Eのガロア群Gの位数は2!=2で2は素数だから、Gは恒等置換と互換の2要素{e,ρ=(1 2)}の巡回群だ。
(途中経過)
f(x)=0の2つの解をα、βとして、p=α+β, q=α-βとする。2次式の因数分解からの発想だ。
この2式で解のかき混ぜをGのρ(ロー)でやってみよう。ρ(α)=βのように、2解は交換される。
・pは対称式なのでαとβを入れ替えても和pは同じだから、そのままでρで不変だね。
・qは対称式ではないからくずれる。これを不変化したい。ρ(q)=(-1)q。
2回ρをすると、ρρ(q)=qになりもどる。
そこで、2回ρする代わりに、qを2回転、つまり、2乗してみる。
q2=(α-β)2=(α+β)2-4αβなら、ρのかきまぜで不変化できた。だから、q∈E、q2∈Fとなる。
q2は有理数であり、解と係数の関係から係数表示ができるし、qは最小分解体、解が出せる体にある。
・つまり、qがあると解を表現できる、解の公式が作れるということだね。
(このq2を判別式Dと名付けることが多いですね。)
あとは、計算問題だ。D=q2=(α-β)2=(α+β)2-4αβ=a2-4bとなる。
連立方程式α+β=a, α-β=±√Dを解いて、x=(p+q)/2、y=(p-q)/2
体の視点で見ると、Eは√Dを添付した拡大体F(√D)ということだね。
α,βをスローに置換してみる
1.3次方程式の解の公式
<スタートとゴールの確認>
さっきの2次方程式のときと同じ流れで取り組んでみよう。
・3次式が1の3乗根で1次式の積に分解できる。
・3!=3*2*1=3*2は3の階乗の素因数分解だ。
・一番カンタンな3次方程式x3=1の解はx=1,ω,ω2で、ω2+ω+1=0で、ω=(-1+√3i)/2
表記をカンタンにするためだけにω2=δとする。δω=1,1+ω+δ=0となるね。
・連立方程式 x+y+z=0, x+ωy+δz=r, x+δy+ωz=sを解くと、x=(0+r+s)/3,y=(0+ωr+δs)/3,z=(0+δr+ωs)/3
この4つの基本から3次方程式の解の公式が作れるでしょう。
(ゴール地点)カルダノの公式(手順)
3次方程式 から、
を作り、2つの解α,βの3乗根 から、3次方程式の解は
または、
を作り、2つの解α,βの3乗根 から、X= 。
(スタート地点)ガロア理論
3次方程式のの3つの解をx,y,zとする。
基礎体はωが自由につかえるようにQにつけてF=Q(ω)。
最小分解体をE=Q(x,y,z)とする。解と係数の関係からxyz=-q, xy+xz+zx=p, x+y+z=0。
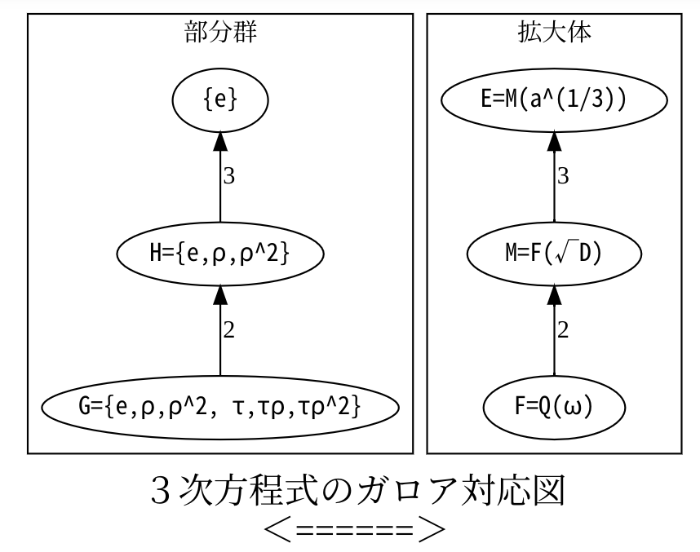
Eのガロア群Gの位数は3!=3*2だからG=S3=C3×C2だ。S3は可解で正規列がS3▷A3▷{1}となるね。
S3の生成元を3次の巡回置換ρ=(1 2 3), 互換τ=(1 2)とすると、ガロア群G=<ρ,τ>={e, ρ,ρ2, τ,τρ, τρ2}。
Gの正規部分群は、H={e, ρ, ρ2}=A3交代群で3解(正三角形の3頂点)をぐるぐる回転する巡回群。
G/H=<ρ,τ>/<ρ>=<τ>={e,τ}は正三角形を裏返すかどうかの巡回群。
<正規部分群Hに対する中間体Mを作るための見通しをたてる>
群Hで動かない中間体H¥=Mは何でしょうか?
G/Hの剰余類群は{0,1}の剰余群,巡回群と同型なので回転を止めれば、裏表の操作だけになるね。
h0,h1の2種で代表させます。
中間体Mの要素でFにない元をm,nについてh1(m)=nとする。2式p=n+m, q=n-mにh1を作用させよう。
2次方程式のときと同様にh1(p)は不変で、h1(q)は符号が反転する。
だから、p=n+m=F数、q=n-m≠F数。
h1((m-n)2)=h1(m-n)h1(m-n)=(n-m)(n-m)=(n-m)2∈Fです。qが2乗で不変化できた。
これから、q=m-n=√F数となり、m,nの和と差からm=(√F数+F数)/2となるね。
だから、M=F(√F)。中間体MはFの平方根をFに添付した拡大体になるということだね。
このあとは、
3つの解x,y,z∈Eに対して、0=x+y+z, r=x+ωy+δz, s=x+δy+ωzとして、
x=(0+r+s)/3,y=(0+ωr+ω2s)/3,z=(0+ω2r+ωs)/3
r,sをf(x)=0の係数p,qで表すことで、解の公式ができるはずだ。
α,βの3乗根u,vを組み合わせて3つの解を作る
<Fに平方根√Dを添付してMを作る>
正規部分群Hにあるかきまぜρで不変な式を作りましょう。
X3+pX+q=0の3つの解をx,y,zとするとき、因数分解の式から3式を作ろう。
0=x+y+z,
r=x+ωy+δz,
s=x+δy+ωz
このうちの2式r,sに巡回ρをしかけたときの変化から、不変化する式を作ろう。
( 表記のカンタンのためにω2=δとする。δ+ω= -1, δω=1。 解と係数の関係から、
xyz=-q, xy+yz+zx=p, x+y+z=0となり、y+z=-x, x3=-px-q, y3=-py-q, z3=-pz-q などを使おう)
rs = (x+ωy+δz)(x+δy+ωz)=x2+y2+z2+(δ+ω)(xy+yz+zx)=(x+y+z)2-2(xy+yz+zx)-(xy+yz+zx)= -3p
r+s = x+ωy+δz+x+δy+ωz=2x+(ω+δ)(y+z)=2x+x=3x
ρ(r)=y+ωz+δx=δ(x+ωy+δz)=δr,
ρ(s)=y+δz+ωx=ω(x+δy+ωz)=ωs。
3回ρをすると、ρρρ(r)=δ3r=r、ρρρ(s)=ω3s=sになりもどる。
そこで、3回ρする代わりに、r,sを3回転、つまり3乗してみる。
ρ(r3)=(ρ(r))3=(δr)3=r3、ρ(s3)=(ρ(s))3=(ωs)3=s3
正規部分群Hのかきまぜρでr3,s3ともに不変だから、r3+s3も不変で中間体Mにある。
不変化が成功したね。あとはこの不変式を係数表示にすればいいね。
ρ(r3+s3)=r3+s3=(r+s)3-3rs(r+s)=(3x)3-3(-3p)(3x)=27x3+27px=27(-px-q+px)=-27q
r3+s3=-27q, r3s3=-27p3
r3,s3はt2+27qt-27p3=0の解ですね。(補助方程式)
M=F(√D)にFを拡大できました。
<Mに3乗根a1/3を添付してEを作る>
r,s =
3つの解x,y,z∈Eに対して、0=x+y+z, r=x+ωy+δz, s=x+δy+ωzとして、
連立方程式を解いた式、
x=(r+s)/3,
y=(ωr+ω2s)/3,
z=(ω2r+ωs)/3
これで、ゴールですね。
質問:3次方程式の解の公式をgeogebraで視覚化するにはどうしたらよいでしょうか。
まず2次方程式x2+ax+b=0の解の公式を作りましょう。
3次方程式のカンタン形のx3+px+q=0を作り、a=q, b=-(p/3)^3の数式を書きます。
p, qはスライダーで整数の可変値にします。
2次方程式の解α、βにしたときにその3乗根の出し方は注意が必要です。
z=α,βを複素数として設定した場合、その3乗根cbrt(z)が予想と違うことがおきます。
z=α,βの虚部が正ならば、3乗根は正しく出せますが、
zの虚部が0で実部が負の数のときは、ただの3乗根関数cbrt(z)が複素数になってしまいます。
偏角が3分の1になり、大きさが3乗根になるからです。
それの防ぎ方は、zの虚部imaginary(z)==0なら、実部real(z)だけを3乗根関数cbrt()に入れましょう。
次は4次方程式の解の公式とガロア理論をつなげたい。
その前にまとめをしておこう。
<解の公式があることの一般化>
F上のn次の一般代数方程式が代数的に解けるのは、代数的解法(Fに四則演算とべき根を有限回を行って、解が表現できる)があること。
・体で見ると、体Fから拡大を繰り返した先に最小分解体Eに到達するべき根拡大の連続になるね。
・群で見ると、ガロア群Gal(E/F)=Snの正規分群がH1,H2,...,{1}まで続き、
商群の位数が巡回群となるときは可解群となることだ。
商群の位数がmならば、m乗根を体に添付して拡大する。
(可解群の商群が「巡回群」を「アーベル群」、「素数位数の群」としても同じこと)
・つまり、商群が巡回群なら、ぐるぐる回してぜんぶの要素が作れる。
ぐるぐる回すかわりにべき乗して不変化すれば、固定体に属する要素が作れる。
不変化式を係数で表すと、解の公式につながる。
・n次方程式のがロア群の商群作りはn!の素因数分解による。
2.4次方程式の解の公式
<スタートとゴールの確認>
さっきの3次方程式のときと同じ流れで取り組んでみよう。
4次式で1次式の積に分解できるものがある。
・
4!=4*3*2*1=3*2*2*2
(ゴール地点) オイラーの方法
・ と因数分解・
を比較して、p=-2(s2+t2+u2)、q=-8stu、r=(p/2)2-4(s2t2+t2u2+u2s2)
a=4s2, b=4t2,c=4u2とおくと、a+b+c=-2p、abc=q2、4r=p2-(ab+bc+ca)から、 (補助方程式)を作る。
3つの解t=a,b,cから、4で割って平方根をとり、s,t,uに戻すと
となる。4次方程式の解は
(スタート地点)ガロア理論
4次方程式の
基礎体はωが自由につかえるようにQにつけといたほうがよい。基礎体F=Q(ω)。
最小分解体をEとする。4つの解をα,β,γ,δとすると、 解と係数の関係から
α+β+γ+δ=0,
αβ+αγ+αδ+βγ+βδ+γδ=p,
αβγ+αβδ+αγδ+βγδ=-q,
αβγδ=r
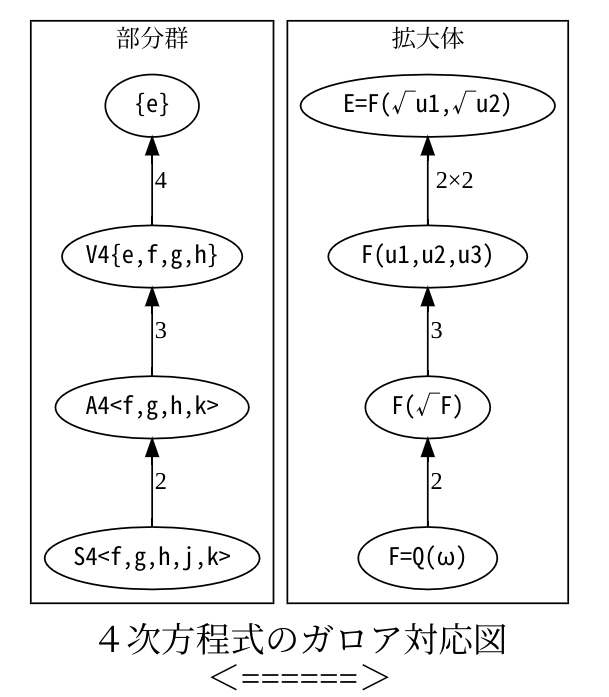
Eのガロア群Gの位数は4!=3*2*2*2だからG=S4=C3×C2×V4だ。
S4は可解でS4▷A4▷V4▷C2▷{1}
対称群S4は4本あみだで、正六面体P6の自己同型作用と同型だね。
生成元は5つ。f=(1 2)(3 4), g=(1 3)(2 4),h=(1 4)(2 3)、j=(3 4)、k=(2 4 3)
ア・4次巡回置換は3×2×1=6個。(1 2 3 4),(1 2 4 3),(1 3 2 4),(1 3 4 2),(1 4 2 3),(1 4 3 2)
互換が2つなら共通要素がない積で4-1=3個。f=(1 2)(3 4), g=(1 3)(2 4),h=(1 4)(2 3) (→偶置換)
イ・互換が1つなら4C2=6個。(1 2),(1 3),(1 4),(2 3),(2 4),j=(3 4)だね。
ウ。互換が2つで1つは不変な3次巡回置換は4×2=8個。(→偶置換)
(1 2 3),(1 3 2), (1 2 4),(1 4 2), (1 3 4),(1 4 3), (2 3 4),k=(2 4 3)
エ・互換の数が0ならeの1個。(→偶置換)
P6の作用
ア・2対面の中心を結ぶ6÷2=3軸で90度の1、2、3倍回転する、3×3=9個。
イ・対辺の中点どうしを結ぶ4×3÷2=6軸での180度回転で6個。
2対辺を含む平面内の2対角線が交換されるが、残りの対角線は上下反転するが自分と重なる。
ウ・主対角線、4軸での120度の1、2倍回転する、4×2=8個。
S4の可解列
V4 = <f、g、h>={e,f,g,h}
A4 = <f、g、h、k>={e,f,g,h}+{e,f,g,h}k+{e,f,g,h}k2
W1 = <f>={e,f}, W2=<g>={e,g}, W3 = <h>={e,h}
<中間体を作る>
商群の指数はS4/A4=24/12=2、A4/V4=12/4=3、V4/{1}=4
指数が3の拡大があるので、3次方程式の解の入れ替えにそなえ基礎体をF=Q(ω)とする。
・群A4に対する中間体はKは、S4/A4=2だから2次拡大。S4/A4={e,f} = C2 3次方程式のときと同様に√Fの数をFに添付する。群A4に対応する中間体はK=F(√F)
・群V4に対応する中間体は、A4/V4=3だから3次拡大だね。A4/V4={e,k,k2} = C3
f(x)=0の4つの解α,β,γ,δでつくる3つの式u1,u2,u3でV4の作用fで不変な要素を作ろう。
V4 = <f=(1 2)(3 4), g=(1 3)(2 4),h=(1 4)(2 3)>={e,f,g,h}
u1=(α+β)(γ+δ), u2=(α+γ)(β+δ), u3=(α+δ)(β+γ) とおくと、
f(u1)=u1,
f(u2)=u2,
f(u3)=u3,......のようにして、
u1,u2,u3はV4の不変だから、V4に対応する中間体はM=K(u1,u2,u3) 解と係数の関係を満たす3次方程式を作ろう。詳しい計算は省略。。。。
ここで(t-u1)(t-u2)(t-u2)=
u1+u2+u3=-2p
u1u2+u2u3+u3u1=p2-4r
u1u2u3=q2
これで、t=u1,u2,u3が求められる。
・いよいよ、最後の拡大に入る。W1 = <f>={e,f}, W2=<g>={e,g}, W3 = <h>={e,h}
群W1,W2,W3に対応する中間体は、V4/Wi=2だから2次拡大だね。
Wiに対応する中間体はu1,u2,u3の平方根をMに添付して、M(√u1),M(√u2),M(√u3)の3系統の拡大体。
さらに、それらをすべて含むのがゴールの最小分解体N=M(√u1,√u2,√u3)
連立方程式u1=(α+β)(γ+δ), u2=(α+γ)(β+δ), u3=(α+δ)(β+γ) を解こう。
α+β+γ+δ=0と解と係数の関係から、
α+β, γ+δは(α+β)+(γ+δ)=0,(α+β)(γ+δ)=u1から、x2=u1の解、
α+γ, β+δは(α+γ)+(β+δ)=0,(α+γ)(β+δ)=u2から、x2=u2の解、
α+δ,β+γは(α+δ)+(β+γ)=0,(α+δ)(β+γ)=u3から、x2=u3の解 。
だから、α+β, γ+δ=√u1, -√u1、α+γ, β+δ=√u2, -√u2、α+γ, β+δ=√u3, -√u3
実際は、u1u2u3=q2 解と係数の関係が使える。u1,u2から、√u3は決まるので、N=M(√u1,√u2,√u3)=M(√u1,√u2)
連立方程式を解けば、
α=(√u1+√u2+√u3-(-√u1-√u2-√u3)/2)/3=( √u1+√u2+√u3)/2
β=√u1-(√u1+√u2+√u3)/2=( √u1-√u2-√u3)/2
γ=√u2-(√u1+√u2+√u3)/2=(-√u1+√u2-√u3)/2
δ=√u3-(√u1+√u2+√u3)/2=( √u1-√u2+√u3)/2
最後の拡大はV4の拡大だれど、4=2×2より、3次方程式の3つの解u1,u2,u3
から適当に2つ選び、それぞれの解√ui, √ujを添付する拡大だから、2次拡大を独立に2つ行うことになる。だから4は素数ではないが、素数2の拡大を別々に2つやることになる。
拡大次数はM=K(u1,u2,u3)に対して、2×2=4であって、N=M(√ui, √uj)ということだね。