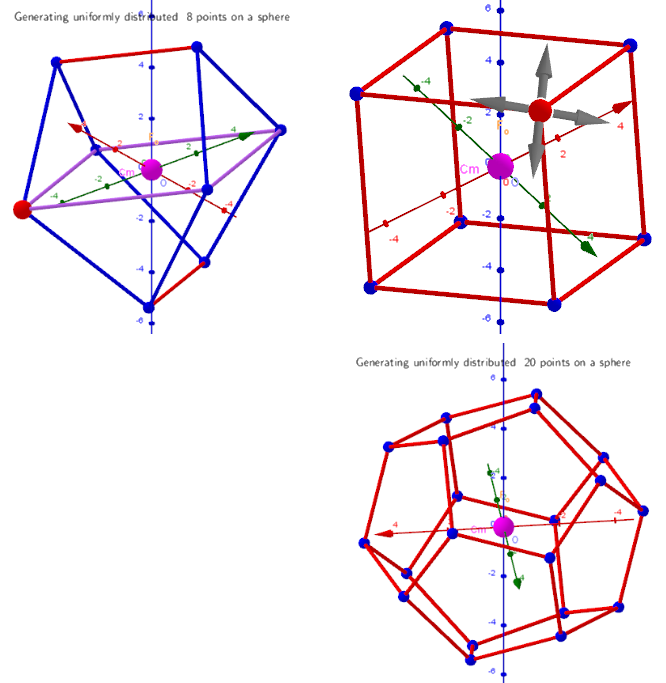
Installation of extreme distributions of the vertices of the polyhedra Cube, Gyrobifastigium, Dodecahedron by fixing their two antipodal vertices.
The applet contains many examples of extreme distributions. The iterative procedure used finds mainly the distribution corresponding to the global maximum, regardless of the initial particle distribution. Other solutions can be found under certain restrictions of the initial distributions.
This applet shows cases where two antipodal points are fixed (n1=2). By clicking on the "Cube or Gyrobifastigium" button, depending on the initial random distribution of points, the iterative procedure finds Gyrobifastigium (J26) p=1.478 763 285 or Cube p=1.480 440 157 243 444. Since the average distance p between particles on the unit sphere is larger for the cube, when you click this button repeatedly, the cube will be installed more often. Vertex A can be fixed at any point of the sphere.
Using the extreme distribution for the cube (the number of pinned points n1=8), clicking on the "Dodecahedron" button installs its extreme distribution.