Función Cuadrática - Tiro Perfecto
Introducción
A) La parábola, "curva color naranja" representa la trayectoria de un balón hacia un tablero de básquet, donde los puntos amarillos definen la distancia horizontal y es la altura correspondiente del tablero. La curva muestra la trayectoria que deberás encontrar.
B) La trayectoria de un segundo lanzamiento "curva color rojo" representa la función que debe de coincidir con la primera curva. Modelo que debes de determinas
C) Para encontrar la ecuación deberás de encontrar el valor de a, b y c de la ecuación cuadrática modelada.
C1. Si no te sale con exactitud los valores de a y b, activa el código 1970 para comparar los resultados y determina el porcentaje de error de tus resultados.
D) Además, tienes 7 puntos, que podrás utilizarlo para poder encontrar la función cuadrática, que representa la trayectoria de tu balón.
Nota: Saldrá el sonido de la narración del lanzamiento sólo si logras un tiro perfecto
A partir de la ecuación determinada deberás de:
Hallar el eje simétrico y la altura máxima del balón. (Casilla de entrada)
Escribir el punto vértice de la trayectoria del balón. (Casilla de entrada)
Escribir la función cuadrática de la forma canónica. (Casilla de entrada)
Hallar los puntos ceros de la función. (Casilla de entrada)
Escribir la función cuadrática de la forma factorada. (Casilla de entrada)
Comparar las gráficas de la práctica
USA EL CUADRO DE ANÁLISIS DE UNA FUNCIÓN CUADRÁTICA, PARA PODER CUMPLIR EL RETO
Guía para el uso del control
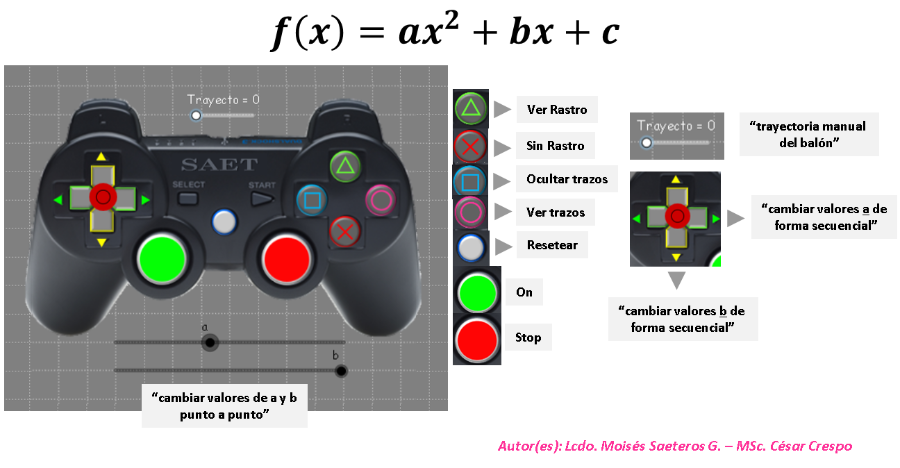
EJERCICIO # 1
Considere la función , que se muestra en el siguiente gráfico.
EJERCICIO # 2
El gráfico de una función cuadrática f(x) se muestra a continuación.
EJERCICIO # 3.
Considere la función f(x) = -2 ( x - 1)( x + 3 ), para . La siguiente figura muestra una parte del gráfico de f.
Para este gráfico de f:
La función f se puede escribir en forma f(x)= -2(x - h)2 + k.
EJERCICIO # 4
Una fábrica elabora camisas. El costo, C, en dólares de Fiji (FJD), de producir x camisas está modelado por
f(x)=(x - 75)2 + 100
El costo de producción no debe pasar los 500 FJD. Para lograrlo, la fábrica tiene que producir al menos de 55 camisas y como mucho s camisas.
EJERCICIO # 5
Bella lanza una pelota desde la parte superior de una pared hacia un suelo plano y horizontal. La trayectoria de la pelota está modelada por la curva cuadrática y = 3 + 4x - x2, donde x representa la distancia horizontal que se lanza la pelota e y representa la altura de la pelota sobre el suelo. Todas las distancias se miden en metros. La pared se encuentra a lo largo del eje y. La curva corta el eje y en el punto A y tiene su vértice en el punto B.
EJERCICIO # 6
Victoria utiliza unos ejes de coordenadas para dibujar el diseño de una ventana. La base de la ventana está en el eje x, la parte superior de la venta tiene forma de curva cuadrática y los lados son lineales verticales, tal y como se muestra en la figura. Los extremos de la curva son los puntos (0, 10) y (8, 10), y el vértice de la curva está en (4, 12). Las distancias vienen dadas en centímetros.
La curva cuadrática se puede expresar en la forma y = a x2 + b x + c, para .
