Dynamische Geometriesoftware kennenlernen
Grundfunktionen einer DGS
a) Zeichne die Punkte A(3|1) und B(-2|-1) in das Koordinatensystem.
b) Zeichne eine Gerade g durch die Punkte A und B.
c) Zeichne den Punkt C(1|-2) in das Koordinatensystem.
d) Zeichne eine zu g parallele Gerade h, die durch den Punkt C verläuft.
e) Zeichne eine zu g senkrechte Gerade, die durch den Punkt C verläuft.
f) Zeichne einen Punkt D so ein, dass die Figur ABCD ein Parallelogramm ergibt.
g) Zeichne das Parallelogramm als Figur ein.
h) Miss die Länge der gegenüberliegenden Strecken des Parallelogramms.
Spiegelung mit DGS
Zeichne das Dreieck mit den Eckpunkten A(1|1), B(2|1) und C(1|4) in das Koordinatensystem.
a) Spiegle das Dreieck an einer Gerade durch die Punkte D(5|1) und E(4|4).
b) Zeichne drei zur Spiegelachse senkrechte Geraden, die durch die Punkte A, B und C verlaufen.
c) Wähle "Bewege" und ziehe den Punkt B auf die Koordinaten (4|-1). Beobachte die Veränderungen und gib die veränderten Koordinaten von B'' an.
Gib die veränderten Koordinaten von B'' an.
Verschiebung mit DGS
a) Zeichne einen Verschiebungspfeil vom Punkt A(-5|4) zum Punkt B(-1|1).
b) Zeichne das Trapez mit den Eckpunkten C(-2|-1), D(3|-1), E(2|2) und F(0|2).
c) Verschiebe das Trapez CDEF um den Verschiebungspfeil.
d) Verschiebe das Trapez so, dass C'' im Koordinatenursprung liegt. Gib die Koordinaten von E'' an.
Koordinaten von E''
Komplexe Aufgabe
a) Spiegle die Figur ABCDE an der x-Achse.
b) Die gespiegelte Figur wird so verschoben, dass D' auf Z liegt.
c) Leo behauptet: "Ich kann die verschobene Figur mit zwei Spiegelungen wieder in die Figur ABCDE überführen." Überprüfe, ob Leo recht hat.
Weiterführende Aufgaben
Bearbeite die nachfolgenden Aufgaben mit DGS.
Aufgabe 1

Aufgabe 2
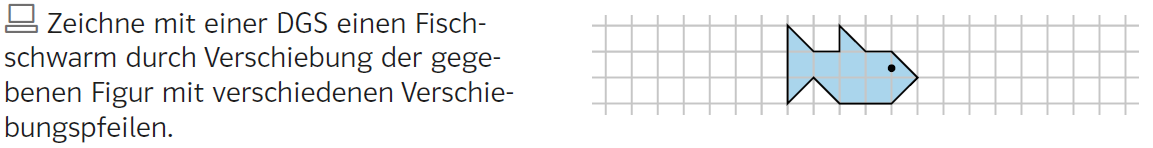
Aufgabe 3

Aufgabe 4
