Geometric median 2D. Eine dynamische Konstruktion des Fermat-Punktes im n-Eck mit Hilfe von der Weiszfeld- Iterationsverfahren
Das ist eine bekannte historische Optimierungsaufgabe:
Es gibt n-Konsumenten. Es ist erforderlich, einen Punkt zu finden, bei denen die Summe der Abstände zu den n-Konsumenten minimal wird. Dieser Punkt wird als Fermatpunkt benannt nach dem französischen Rechtsanwalt und Mathematiker Pierre de Fermat(1601-1665). Das Problem hat exakte Lösung im Fall n = 3. Im allgemeinen Fall gibt es eine numerische Lösung: Weiszfeld(1916–2003 geboren in Budapest) -Iterationsverfahren der Koordinatenbestimmung des Fermat Punktes.
Geometric median, Euklidischer minisum-Punkt: https://en.wikipedia.org/wiki/Geometric_median
For a given set of n points x1, x2, ... , xn with each xj∈ ℝ2 , the geometric median is defined as
argmin, μ∈ ℝ2, where denotes the Euclidean norm.
Here, argmin means the value of the argument which minimizes the sum. In this case, it is the point μ from where the sum of all Euclidean distances to the xi's is minimum.
If μ is distinct from all the given points, xj, then μ is the geometric median if and only if it satisfies:
- the conditions for a local optima: first-order partial derivatives must equal zero.
The right side of the equation in this applet is designated as Δ.
This is equivalent to: (iteration formula), which is closely related to Weiszfeld's algorithm. This method converges for almost all initial positions.
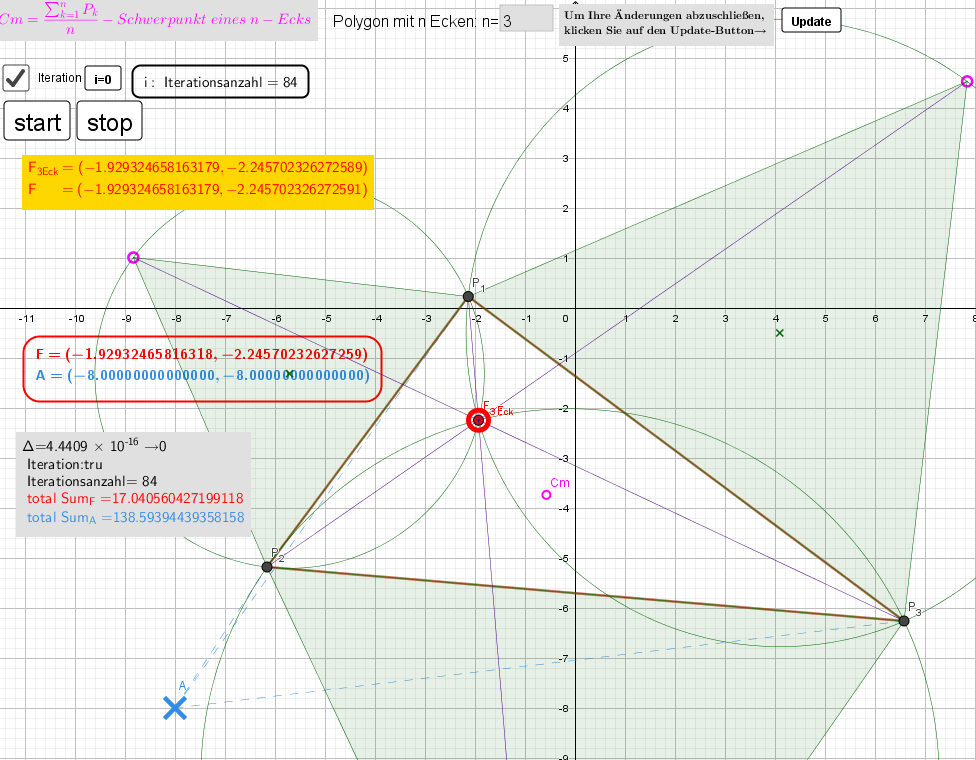
Ich habe diesen Algorithmus in Form eines Geogebra-Skripts implementiert (hier F:=μ).
Schieberegler a: Execute[ { "F=CopyFreeObject[Sum[Zip[(r/ Length(r - F)),r,lP ]] / Sum(Zip(1 / Length(a - F), a, lP))] ","SetValue[Lä, Length[F-R_1]]" ,"SetValue(R_1,F)"} ].
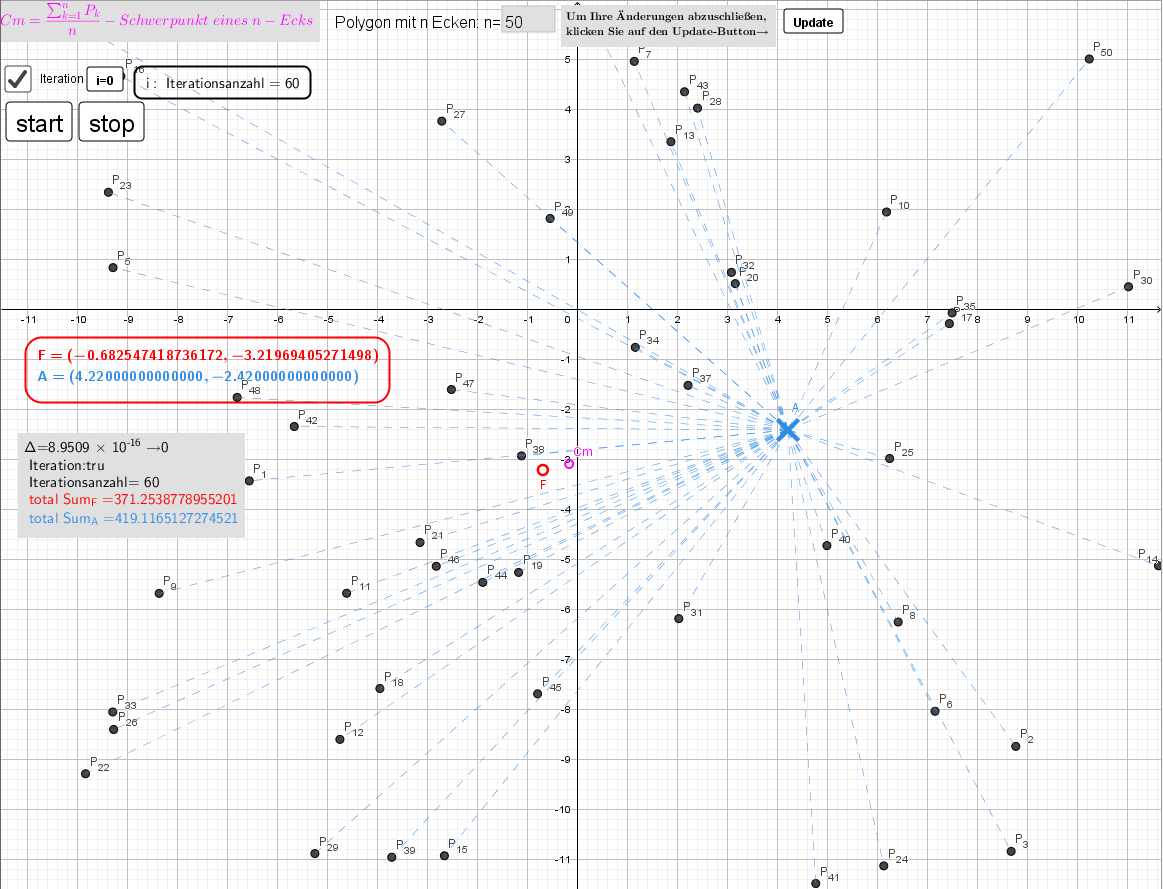
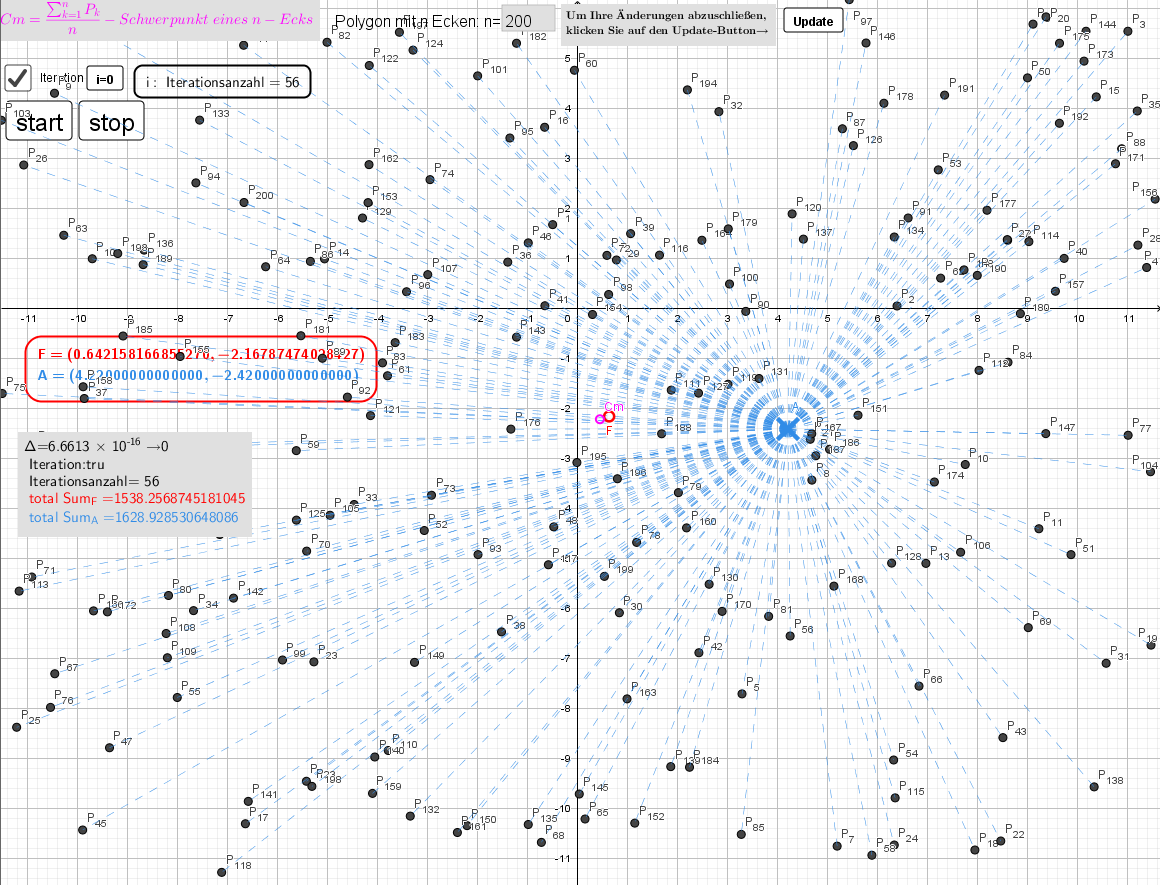
Das Konvergenzverhalten des iterativen Berechnungsprozesses wird als Statusmeldungen laufend angezeigt. Die Methode zeigt eine gute Konvergenz für Polygons mit n=3,...,200 Eckpunkten .
Die Animation zeigt mehrere Iterationsschritte des Weiszfeld-Verfahrens. Als Ergebnis, wird Punkt F an Fermatpunkt verschieben.
Aufgabe:
Es sei A ein beliebiger Punkt, der mit anderen Punkten verbunden ist. Stellen Sie sicher durch Bewegen des Punktes A, dass der gefundene Fermatpunkt der gewünschte ist: Summe der Abstände zu den Eckpunkten möglichst klein!