Discovery aplicado a la posición 1
Esta actividad pertenece al libro de GeoGebra Inclinando la botella de Piaget con GeoGebra Discovery.
A continuación veremos algunas posibilidades del uso de Discovery, aplicándolos a las dos primeras posiciones de la botella de Piaget que hemos visto (ya que las otras dos son versiones simétricas de ellas).
Queremos que Discovery nos ayude a realizar la construcción que aparece en la actividad Sin alcanzar las bases.
Para ello, abrimos GeoGebra Discovery y desde esa página buscamos la URL de esta actividad (https://www.geogebra.org/m/v8pxegrz). [Alternativamente, también podemos descargar previamente la construcción en nuestro ordenador, pulsando aquí.] GeoGebra Discovery abrirá la construcción que contiene, que es la siguiente (copia de la que aparece en "Sin alcanzar las bases"):
Al realizar esa construcción habíamos razonado que O debía ser el punto medio de H y H', y así lo habíamos definido. Pero ahora queremos que sea Discovery quien no ayude a encontrar tal posición de O, que iguala las áreas de los triángulos OCH y OC'H'.
Para ello, redefinimos O como un punto arbitrario en el segmento HH':
HH' = Segmento(H, H')
O = Punto(HH')
y creamos los segmentos necesarios para comparar las áreas:
OH = Segmento(O, H)
OH' = Segmento(O, H')
HC = Segmento(H, C)
H'C' = Segmento(H', C')
Ahora ya podemos usar el comando EcuaciónLugar. Discovery mostrará el lugar que debe ocupar O para que las áreas coincidan:
EcuaciónLugar(OH HC==OH' H'C', O)
El resultado será similar al que muestra la siguiente imagen. El lugar que encuentra Discovery está situado en el punto naranja.
Nota: El lugar encontrado por Discovery consta además de otro punto, simétrico del anterior respecto a la horizontal que pasa por A. Este tipo de “extra” soluciones, de algún modo simétricas, se da con frecuencia al operar con expresiones algebraicas, que es lo que hace Discovery internamente, y se debe a que el punto A' está definido como un punto de una circunferencia, pero no es posible aislar un solo punto de la misma sin introducir raíces cuadradas, lo que está fuera del marco polinómico en el que GeoGebra Discovery realiza internamente los cálculos correspondientes.
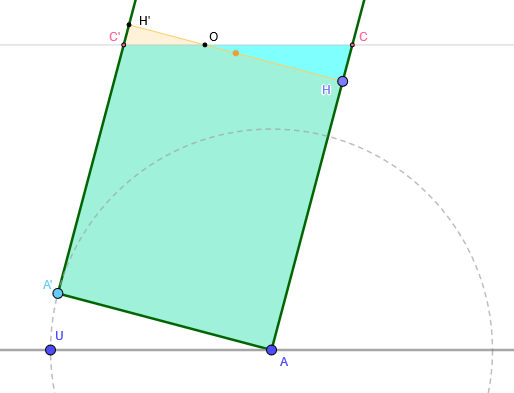
Como vemos, Discovery descubre automáticamente dónde poner O para que los dos triángulos tengan la misma área. Eso sí, el resultado es numérico, ahora nosotros debemos descubrir que ese punto es precisamente el punto medio de HH'… pero eso parece bastante obvio de conjeturar, una vez que tenemos la pista que da Discovery.
Así que borramos el lugar geométrico representado por el punto naranja (para evitar provocar un error en ese lugar geométrico al redefinir O) y volvemos a redefinir O como el punto medio de H y H':
O = PuntoMedio(H, H')
Finalmente, usamos el comando Demuestra para que Discovery confirme nuestra conjetura:
Demuestra(OH HC==OH' H'C')
Veremos aparecer en la Vista Algebraica un nuevo valor lógico con este resultado: true ■
Nota: Alternativamente, podemos usar el comando DemuestraDetalles: DemuestraDetalles(OH HC==OH' H'C')
En tal caso, veremos aparecer en la Vista Algebraica una nueva lista con este resultado: {true, {"SonIguales[A, U]"}} que especifica que la igualdad queda demostrada siempre que los puntos A y U no sean iguales (construcción degenerada).