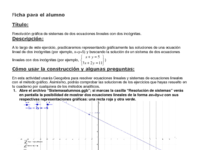
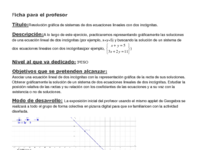
Resolución gráfica de sistemas de dos ecuaciones lineales con dos incógnitas.
A lo largo de este ejercicio, practicaremos representando gráficamente las soluciones de una ecuación lineal de dos incógnitas (por ejemplo, x+y=5) y buscando la solución de un sistema de dos ecuaciones lineales con dos incógnitas.
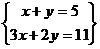
En esta actividad usarás Geogebra para resolver ecuaciones lineales y sistemas de ecuaciones lineales con el método gráfico. Asimismo, podrás comprobar las soluciones de los ejercicios que hayas resuelto en tu cuaderno por cualquiera de los métodos analíticos.
1.Abre el archivo “Sistemasalumnos.ggb”; si marcas la casilla “Resolución de sistemas” verás en pantalla la posibilidad de mostrar dos ecuaciones lineales de la forma ax+by=c con sus respectivas representaciones gráficas: una recta roja y otra verde.
a)Usando los deslizadores sobre cada ecuación, cambia los valores de a , de b y de c en ambas ecuaciones. Observa que, al modificarlos, el programa traza automáticamente las rectas correspondientes.
b)Da los valores: b=b’. ¿Cómo son las rectas cuando ambas ecuaciones tienen el mismo valor en a y a’?
c) Y cuando además de b=b’, a=a’. ¿Qué pasa con las rectas si tienen el mismo valor en c y c’?
2. Cambia los valores de a, b, c, a’, b’, c’ para obtener el siguiente sistema de ecuaciones.
a) Explica por qué las ecuaciones anteriores determinan que las respectivas rectas se corten en un punto.
b) ¿Hay algún punto en el plano que solucione el sistema de ecuaciones, es decir, cuyas coordenadas
(x, y) hagan verdaderas ambas igualdades? Justifica tu respuesta.
3. Desmarca las casillas ”Primera ecuación” y “Segunda ecuación” y marca la casilla “Sistema” para encontrar en verde el punto donde se cruzan ambas rectas. Observa las coordenadas del Punto verde V
a) Escribe las coordenadas del punto donde se intersecan las rectas.
Coordenada en x: Coordenada en y:
b) Verifica que esos valores de x e y resuelven ambas ecuaciones. Explica por qué.
c) Cambia los valores de a, b, c, a’, b’, c’ para generar un sistema de ecuaciones sin solución. Explica tu procedimiento.
d) Inventa un sistema de ecuaciones cuya solución sea el punto (1, 1). Escríbelo a continuación y explica cómo lo obtuviste.
e) Inventa dos sistemas de ecuaciones: uno que sí tenga solución y otro que no, e intercámbialos con un compañero para que intente resolverlos. Comentad cómo encontrasteis la solución de uno de los sistemas, y por qué el otro carece de ella. Anotad vuestras conclusiones.