Isaac Barrow y el Teorema Fundamental del Cálculo
Isaac Barrow y el Teorema Fundamental del Cálculo
En esta actividad se contempla una ilustración de la versión geométrica del Teorema Fundamental del Cálculo desarrollada por Isaac Barrow en sus lecciones Lectiones Geometricae de 1670 trabajo en el cual colaboró I. Newton. El resultado que trata sobre el TFC corresponde a la Proposición XI de la Lección X y establece lo siguiente:
Proposición: Sea ZGE una curva dada por y=f(x) cuyo eje es VD y consideremos las ordenadas (VZ, PG y DE) perpendiculares a este eje y que crecen continuamente desde la ordenada inicial VZ (Figura 1); sea VIF una curva dada por y=F(x) tal que si una línea recta EDF se traza perpendicular al eje VD, que corta a las curvas en los puntos E, F y a VD en D, el rectángulo determinado por DF y una longitud dada R es igual al área de la región VDEZ; sea T un punto sobre VD talque y únase T y F. Entonces TF toca a la curva VIF en el punto F. 
Figura. 1: Ilustración de. Barrow para la demostración del TFC, (Struit, 1969).
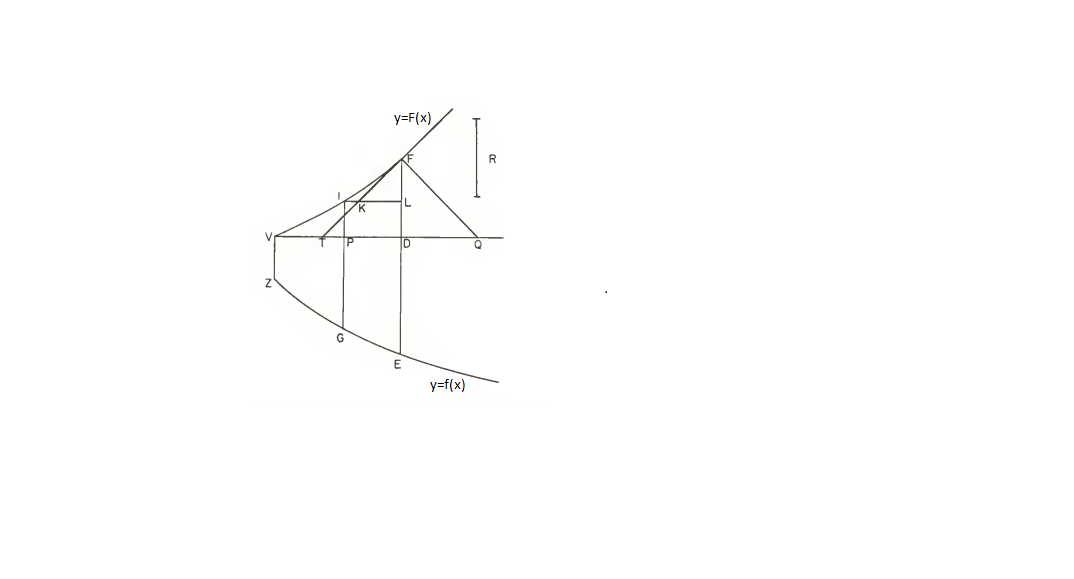
La demostración de este resultado se puede revisar en, Struit, J. D. (1969). Source Book in Mathematics 1200-1800. Cambridge, Mas: Harvard University Press, y fundamentalmente consiste en demostrar que la recta TF está siempre por debajo de la curva VIF.
Si se interpreta, en notación actual, lo que muestra la Figura 1, se tiene que la curva ZGE se expresa por una función y = f(x), la curva VIF se representa por y = F(x). El segmento VD representa el eje de abscisas donde toma valores x. La cantidad F(x) representa el valor del área bajo la gráfica de f comprendida entre el punto V y x. Dado un punto de abscisa D, Barrow demuestra que la pendiente de la tangente a y= F(x) en el punto F, es decir en el punto (D, F(D)), es igual a f(D) = DE.
En la siguiente actividad se ilustra este resultado y se interpreta en terminología moderna. En la casilla de entrada se define la función y=f(x) considerada y esta se puede modificar a voluntad. Al ir activando los botones se va desarrollando cada paso de la ilustración.