Límite de una función en un punto

Autor:Instituto Geogebra de Castilla y León

Tema:Límites

Explora la idea de límite, seleccionando una función y pulsando sucesivamente en las casillas, según se indica en el texto que aparece tras el applet.

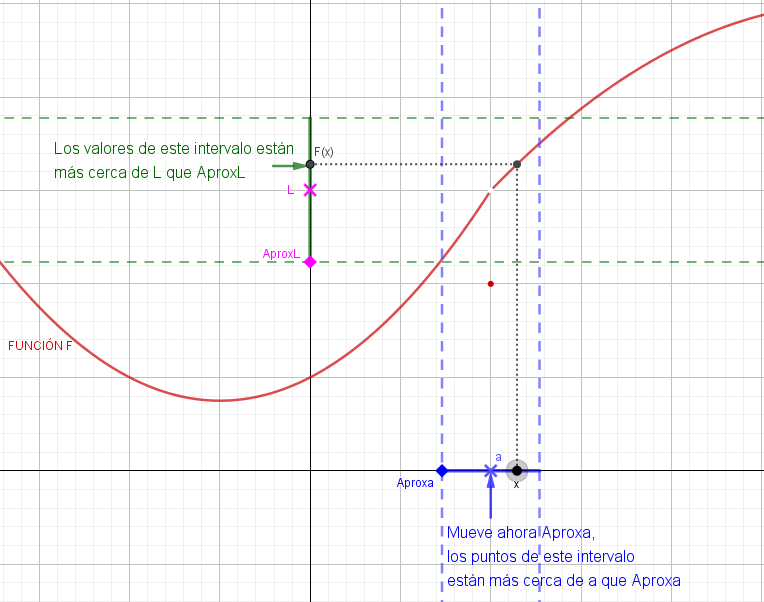
1.- Escoge la función F. Marca las dos primeras casillas de forma consecutiva y sigue las instrucciones.

¿Existe un único valor al que se aproximan las imágenes de los puntos cercanos a "a" pero distintos de "a"?

Marca todas las que correspondan

A
Las imágenes se aproximan a muchos valores pero hay uno que parece mejor que los demás.
B
Dependiendo de si x es mayor o menor que "a", las imágenes se aproximan a un valor o a otro diferente.
C
No hay un valor al que se aproximen las imágenes.

Revisa tu respuesta (3)

2.- Desmarca las dos primeras casillas y marca la tercera y cuarta de forma consecutiva. Verás un intervalo centrado en el número "L" que hayas elegido.

¿Qué significado tiene la distancia de "L" a los extremos del intervalo? (Puede haber más de una opción)

Marca todas las que correspondan

A
Es el error que se comete al aproximar "L" por AproxL
B
Es una cota de error para valorar si una aproximación de "L" es mejor que AproxL
C
Es una aproximación a "L"
D
Es la mitad del tamaño del intervalo pero no tiene relación con las aproximaciones

Revisa tu respuesta (3)

3.- Desmarca la tercera casilla y marca la quinta. Ahora ves también un intervalo centrado en "a".

Tienen alguna relación los intervalos centrados en "L" y en "a"

Marca todas las que correspondan

A
No tienen nada que ver, cada uno está en un eje y controla aproximaciones de números distintos
B
Se relacionan a través de la función puesto que ésta actúa como vínculo de los puntos del eje X con los del eje Y

Revisa tu respuesta (3)

4.- Ajusta Aproxa para que los valores de "x" del intervalo centrado en "a" se "proyecten" a través de la función en el intervalo centrado en "L".

¿Es posible ajustar siempre el intervalo centrado en "a" (entorno reducido de "a") para que las imágenes de TODOS sus puntos estén dentro del entorno de "L", mejorando así Aprox L, aunque AproxL esté muy cerca de "L"?.

Marca todas las que correspondan

A
Es posible siempre
B
Es posible para esta función en este punto
C
No es posible siempre, sólo si el entorno de L es lo suficientemente grande

Revisa tu respuesta (3)

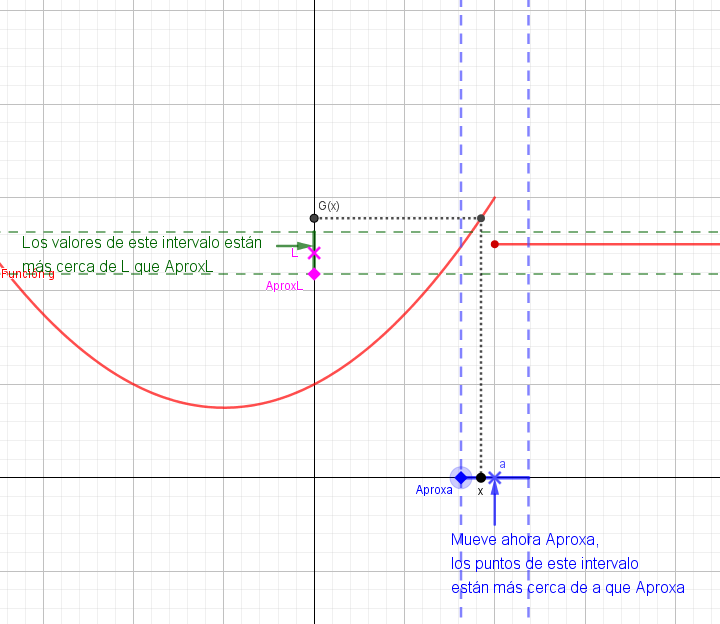
5.- Ahora escoge la función G. Marca las dos primeras casillas de forma consecutiva y haz lo mismo que antes.

¿Existe un único valor al que se aproximan las imágenes de los puntos cercanos a "a" pero distintos de "a"?

Marca todas las que correspondan

A
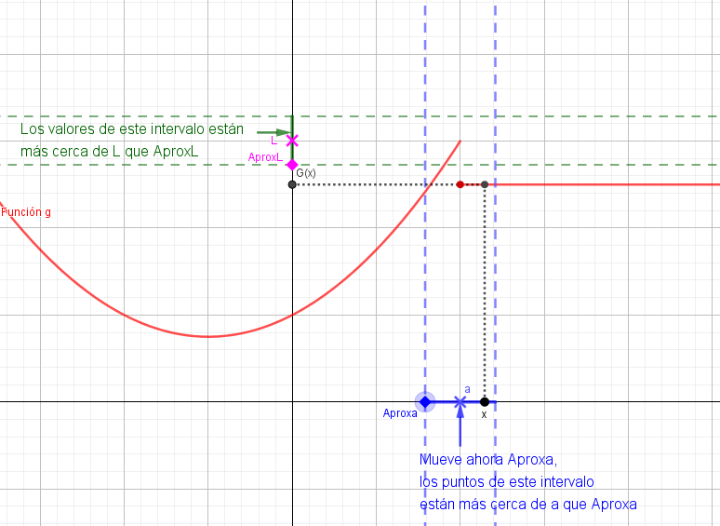
Las imágenes se aproximan a muchos valores pero hay uno que parece mejor que los demás.
B
Dependiendo de si x es mayor o menor que "a", las imágenes se aproximan a un valor o a otro diferente.
C
No hay un valor al que se aproximen las imágenes.

Revisa tu respuesta (3)

6.- ·Escoge un valor para L y mueve AproxL muy cerca de L, marca solo las casillas cuarta y quinta y ajusta Aproxa para que los valores de "x" del intervalo centrado en "a" se "proyecten" a través de la función en el intervalo centrado en "L".

Marca todas las que correspondan

A
Es posible siempre
B
Es posible para esta función en este punto
C
No es posible siempre, sólo si el entorno de L es lo suficientemente grande

Revisa tu respuesta (3)

6.- ·Escoge un valor para L y mueve AproxL muy cerca de L, marca solo las casillas cuarta y quinta y ajusta Aproxa para que los valores de "x" del intervalo centrado en "a" se "proyecten" a través de la función en el intervalo centrado en "L".

Marca todas las que correspondan

A
Es posible siempre
B
Es posible para esta función en este punto
C
No es posible siempre, sólo si el entorno de L es lo suficientemente grande

Revisa tu respuesta (3)

7.- Conclusión

Se ha visto que el límite es el valor al que "mejor" se aproximan las imágenes al aproximarse los valores de "x" a "a", en el sentido de que cualquier aproximación del límite se puede mejorar con las imágenes de todos los valores suficientemente próximos a "a". Si siempre se pueden mejorar las aproximaciones a "L" con las imágenes de todos los valores de un entorno de "a". Es el caso de la función F como se ve en el gráfico siguiente. Se dice que L ES EL LÍMITE DE F EN "a"

Si por el contrario, se puede encontrar una aproximación del "candidato a límite" tal que por muy cerca que se esté de "a" hay imágenes que están más lejos (que no están en el entorno), entonces ese valor no es el límite. Es el caso de la función G. Ninguno de los valores a los que parecen aproximarse las imágenes de puntos cercanos a "a" cumplen dicha condición, como se ve en las dos imágenes siguientes, así que G NO TIENE LÍMITE EN "a".

8. FORMALIZACIÓN

Vamos a dar un paso más a partir de la definición anterior. ¿Qué significa mejorar la aproximación de "L" o de "a"? (Puede haber más de una respuesta correcta)

Marca todas las que correspondan

A
Tener un error menor que dicha aproximación
B
Pertenecer al intervalo centrado en "L" o "a" y radio
C
Que el número tiene menos cifras significativas

Revisa tu respuesta (3)

DEFINICIÓN DE LÍMITE DE UNA FUNCIÓN f EN UN PUNTO a.

Teniendo en cuenta que el error es la diferencia, en valor absoluto entre el número y su aproximación se puede traducir la definición como sigue: Se dice que L es el límite de la función f en a si cumple 1 o 2:

Fijado un entorno E(L,e)), existe otro entorno reducido E*(a,d) tal que para todo x que pertenezca a E*(a,d) entonces f(x) pertenece a E(L,e).
Fijado un valor positivo e (el radio del entorno o cota de aproximación para "L"), existe otro valor positivo d (el radio del entorno o cota de aproximación para "a") tal que para todo x tal que 0<|x-a|<d se cumple que |f(x)-L|<e

Actividad realizada por Sonsoles Blázquez, miembro del Instituto Geogebra de Castilla y León

Límite de una función en un punto

Explora la idea de límite, seleccionando una función y pulsando sucesivamente en las casillas, según se indica en el texto que aparece tras el applet.

1.- Escoge la función F. Marca las dos primeras casillas de forma consecutiva y sigue las instrucciones.

2.- Desmarca las dos primeras casillas y marca la tercera y cuarta de forma consecutiva. Verás un intervalo centrado en el número "L" que hayas elegido.

3.- Desmarca la tercera casilla y marca la quinta. Ahora ves también un intervalo centrado en "a".

4.- Ajusta Aproxa para que los valores de "x" del intervalo centrado en "a" se "proyecten" a través de la función en el intervalo centrado en "L".

5.- Ahora escoge la función G. Marca las dos primeras casillas de forma consecutiva y haz lo mismo que antes.

6.- ·Escoge un valor para L y mueve AproxL muy cerca de L, marca solo las casillas cuarta y quinta y ajusta Aproxa para que los valores de "x" del intervalo centrado en "a" se "proyecten" a través de la función en el intervalo centrado en "L".

6.- ·Escoge un valor para L y mueve AproxL muy cerca de L, marca solo las casillas cuarta y quinta y ajusta Aproxa para que los valores de "x" del intervalo centrado en "a" se "proyecten" a través de la función en el intervalo centrado en "L".

7.- Conclusión

8. FORMALIZACIÓN

DEFINICIÓN DE LÍMITE DE UNA FUNCIÓN f EN UN PUNTO a.

Nuevos recursos

Descubrir recursos

Descubre temas