The motion under a central force by Newton

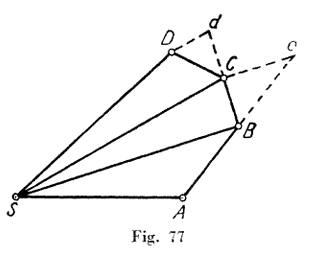
By a very simple and direct geometrical argument, Newton in his Principia established that the motion of a material point that is subject to a central force was contained in a plane, and followed the law of areas which Kepler had formulated in a semi-empirical way (the radius vector sweeps through equal areas in equal times). Below is Newton's argument (see Fig. 1). Carry out the geometric construction proposed by Newton to demonstrate the movement of a point under the influence of a central force.

Suppose the time to be divided into equal parts, and in the first part of that time, let the body by its innate force describe the right line AB. In the second part of that time, the same would (by Law I), if not hindered, proceed directly to c, along the line Bc equal to AB; so that by the radii AS, BS, cS drawn to the centre, the equal areas ASB, BSc, would be deseribed. But when the body arrived at B, suppose that a centripetal force acts at once with agreat impulse, and turning aside the body from the right line Bc, compells it afterwards to continue its motion along the right line BC. Draw cC parallel to BS meeting BC in C; and at the second part of the time, the body (by Cor. I of the laws) will be found in C, in the same plane, with the triangle ASB. Join SC, and, because SB and Cc are parallel, the triangle SBC, will be equal to the triangle SBc, and therefore also to the triangle SAB.