イデアルは理想である

Argomento:Algebra, Dilatazione, Triangoli equilateri, Moltiplicazione, Quadrato

1.倍数からイデアルへ

このワークシートはMath by Codeの一部です。 環から始まり、整域、ユークリッドの整域、体と環を一般から特殊へと狭めてきたね。そのときの鍵を思い出そう。ゼロでないゼロ因子がないのが整域だった。整域だと簡約法則という割り算が使えた。さらに、割り算と余りの原理、整除原理が成り立つのがユークリッド整域だった。そした、余りのある割り算を飛び越して逆元の存在に飛び込んだのが体だったね。こうして振り返ると、いかに割り算が大切かわかるね。小学校３，４年で学ぶ割り算から始まり、分数・小数の理解、割合の理解、逆算の理解、速さの三公式の理解、割合の公式の理解、比と比例式の理解へとつながってきていたね。だから、環でも割り算は大切だ。整数環で割り切れる数といえば、倍数だ。整数の世界では偶数奇数がとても重要で、同じ意味で、倍数による余りによる分類も重要だった。つまり、集合を割り算で分類するという発想が整数環では大切だった。もちろん、群の世界でも、倍数の集合が正規部分群、写像の核になって、同型写像を作ったりした。さて、この超重要な、倍数と余りの関係性が、整数環から一般の環へ、どのように一般化できるだろうか。その鍵がイデアルideal、アイディール、理想数？だ。

ガウス格子点を(zp) と(zp) +1の２色にぬりわける。

アイゼンシュタイン格子点を(zp)-1,(zp),(zp)+1の3色でぬりわける

＜イデアルの定義＞ 環(R,+,×)で同値関係~を a~b,c~dなら、和の保存（a+c~b+d)、反元の保存（-a~-b)、積の保存(a×c~b×d)が成り立つとしよう。０と同値な集合B={x|x~0}とすると、x+y~0+0=0∈B, -x~0∈B, xy~0×0=0∈Bとなり、 和と積と反元で閉じている。このようなBを環Rのイデアルという。 Bがイデアルなら＜B,＋＞は群＜R,＋＞の正規部分群になる。作り方の１つは倍数の集合と同様に、Rから１要素ｍをとり、ｍの倍元の集合をBとすればよい。これをmの倍元とする単項イデアルといい、(m)とかく。mを生成元ともいう。他の作り型はRからいくつかの有限個の要素a,b,...をとり、各要素の倍元の和、積和の集合 ax+by+....をBとすればよい。これをa,b,...からの有限生成イデアルといい、(a,b,...)と生成元を並べてかく。 (イデアルの別の定義）環Rの部分集合Bで加法で閉じていて、 Rのどの数をBにかけても閉じているものを環Rのイデアルという。整数環Zのイデアルは整数aの倍元のあつまりで、aZと書ける。aZ=(a)ともかく。和と定数倍で閉じているというのは、線形空間の部分空間のときと同じような約束だね。・環Rに対して、｛ゼロ｝、R自身を自明なイデアルという。どちらでもないものを真のイデアルという。（例）Zには３がある。3Zは３の倍数の集合は単項イデアル（３）だ。 （例）多項式Z[X]にはf(X)=x+1がある。(x+1)R[X]は、(x+1)の倍元の集合は単項イデアル（(x+1))だ。 （例）ガウス整数Z[i]には2+iがある。2+iの倍元のあつまり・模様は、単項イデアル（2+i)だ。 取り出した要素をmとしたとき、Bはｍの倍元の集合になるので、 B={mx | m, x∈A}={0,±m, ±2m,....}となる。同値関係を≡とかくとしたら、a≡ bなら、aーb≡0　∈B。ｘを含む同値類はB+xとかける。これは、ｍの倍数による剰余系と同じ書き方だね。 結局、イデアルというのは剰余系の０に当たる数の集まり、倍数の集まりの一般化だとわかるね。 （例）整数環ZはB=（３）を法として数直線はB,B+1.B+2の3種類に色分けできる。（例）ガウス整数Z[i]はB＝(1+i)を法としてB、B+1の２種類に色分けできる。（例）アイゼンシュタイン整数Z[ω]はB=(1-ω)を法としてB-1,B,B+1の３種類に色分けできる。

２．環と環の関係

＜部分環＞ 環Aの部分集合Bが加法の部分群で、Bの要素の積も１も、Bに属するときにBは部分環だ。 ・イデアルIが部分環Bに含まれるなら、C=I∩AはAのイデアルになる。　IがBの真の部分なら、CはAの真の部分だ。 ＜環の拡大＞ 大きな環Cの要素ｐをCの部分環Kに添付した要素を係数Kを使ったｐの多項式としてK[p]とする。これを、Kにｐを添付した環という。（例）環Zに√2を添付した多項式は整数係数のΣa_n(√2)ⁿとして表せる。　　この多項式を計算すると、√2の奇数乗は√2が残り、√2の偶数乗は２の倍数になる。　　だから、多項式はｘ＋ｙ√２（ｘ，ｙ∈Z)と表すことができるね。　　この事実はZ[√2]=a√2+b (a,b∈Z)と書ける。（例）R[√2]=a√2+b(a,b∈R）は上記と同様に環となる。（例）Z[

] =a

²+b

+c (a,b,c ∈Z)は環になる。だから、R={ｘ＋

y | x,y∈Z}は環でないね。（例）ガウス整数Z[i]は環Zにiを添付した環だ。（例）アイゼンシュタイン整数Z[ω]は環Zにωを添付した環だね。 ＜環の準同型写像＞ 写像ｆ：環V→環W; x →f(y) とするとき、　f(x+y)=f(x)+f(y), f(x×y)=f(x)×f(y),f(イチｖ)=イチｗが成り立つとき、ｆは準同型写像という。・このとき、f(ゼロｖ）＝ゼロｗとなる。f(-a)=-f(a),f(a-b)=f(a)-f(b)となる。 ・準同型の核Kerf＝{ x | f(x)=0w , x∈V｝はイデアルでもあるね。Kerf≠V。核は和と定数倍で閉じていることは明らかだから、イデアルになる。・準同型の像imf＝{f(x)|x∈V｝はWの部分環になる。・fの逆写像も準同型なら、ｆは同型だ。・V=Wのときは自己準同型・同型というのは群のときと同様だね。　環Vの自己同型全体をAutVなどとかく。AutVは群になり、Aの自己同型群という。・群のときと同じように、ｆが単射であることとKerf＝{ゼロｖ}は同値。 ＜環の準同型定理＞ 群と同様にV/Kerf とimfが全単射の準同型写像になるので、同型になる。＜イデアルによる商環、剰余環＞群Gで倍数にあたる正規部分群Nで割ることにより、G/Nという同値類が商群、剰余群になったように、環Rで倍数にあたるイデアルBで割ることにより、R/Bという同値類は商環、剰余環になる。同値類R/Bの代表元をa,b,cとすると、同値関係は和、積、反元について閉じていて、分配法則にあたるa☓(b＋c)=a☓b＋a☓cが成り立つことは自明。だから、R/Bは環になる。自然な準同型写像ｆ：R→R/B ; x →x + B x+ Bを[x]とか、ｘmod B ともかく。整数のときと同じだね。ｘ−ｙ∈Bならば、x≡y (mod B)　Bの生成元がpなら、x≡y mod pともかいたりする。（例）＜Z/3Z, ＋,☓＞={[0],[1],[2]}は、環/イデアル＝商環。　　　整数Zに3で割った余りr=0,1,2を対応させる写像をhとする剰余系（剰余類）で、　　　加法と乗法が通常の整数計算のようにできるということだね。　　　Z-r∈(3)、h(Z)=h(r+(3))=h(r)+h((3))=r+0=r （例）＜Z[i]/(1+i),＋,☓＞＝{[0],[1]}も商環。ガウス格子点は２色にぬりわけられる。（例）＜Z[ω]/(1-ω),＋,☓＞＝{[-1],[0],[1]}も商環。アイゼンシュタイン格子点は３色にぬりわけられる。 （例）＜R[x]/(1+x²),＋,☓＞= R[i] も商環。イデアルJ=(1+x²)によって、虚数単位は類ｘ＋Jが表す。　　　実数係数の多項式R[X]に既約なx²+1で割った余りR1=a+bxを対応させる写像をｈとすると、　　　１次式R1の加法と乗法となるね。　　　R[x]- R1∈((x²+1))、h(R[X])=h(a+bx+(x²+1))=h(a)+h(b)h(x)+h((x²+1)))=a+b*h(x) h(x)=iとおくと、h(R[X])=a+biでh(x²+1)=0だからi²=h(x)²=-1となるので形式としては、剰余a+bxのaが実部、bが虚部として機能するということだ。（例）＜Z[x]/(1+x²),＋,☓＞= Z[i] も商環。 (１+x²)は、準同型写像 f:多項式Z[x]->ガウス整数Z[i] ; x→i の核だ。x²+1∈Kerf。　　　だから、f(x)∈Kerfとすると、f(x)=g(x)(x²+1)+ax+b (g(x)∈Z[x], a,b∈Z)とできる。　　　そこでもx→iとしたら、f(i)=a0+b=0だから、a=b=0となるから、Kerf={ゼロ式}なので同型　　　Z[x]/(1+x²)はZ[i]と同型だね。 ＜商環から体へ＞ ユークリッド整域Rの素元ｐの単項イデアル(p)で割った同値類、商環R/(p)は体になる。これは、すごいね。Rはただの環じゃダメだ。割り算の商と余りを作れないとね！（例）Zはユークリッド整域で、素数ｐに対して、Z/(p)は体。この体をFpとかく。有限体の典型例だ。（例）Z[x]はユークリッド整域で、x+1は素元だから、Z[X]/(x+1)は体。 （例）Z[i]はユークリッド整域で、７は素元だから、Z[i]/(７)は体。　　上の例から、Z[x]/(1+x²)はZ[i]と同型。なので、Z[i]/(7)同型Z[x]/(1+x²,7)同型F7[x]/(1+x²) F7[x]ではｘ＝[0,1,2,3,4,5,6}のとき1+x²≡{1,2,5,3,3,5,2}だから既約な多項式だから、F7[x]/(1+x²)も体。 （例）Z[ω]はユークリッド整域で、2は素元だから、Z[ω]/(2)は体。

３、イデアルどうしの関係

イデアルは集合だから、集合どうしの演算ができるようにイデアルどうしの演算も考えられるね。 I、Jを環RのイデアルとするときI、Jの生成元をa,bとすると、 I、Jは単項イデアルで、I=(a), J=(b)とかける。＜イデアルの和＞ I＋Jを和イデアルという。 I+J={ax+by| x,y∈R｝だから、I+Jは２元a,bを生成元とするイデアルになり、I+J=(a,b)となる。しかも、a,bの最大公約元をGとすると、a,bはGの倍数だから、I+J=(G)ともかけるね。 (a)+(b)=(a,b)=(a)∪(b)=(G(a,b)) 結果的に、I+J=I∪J （例）整数環ZのイデアルA=(6),B=(9)から、A+B={6x+9y | x,y}

3Zだから、A+B=(3) ＜イデアルの積＞ IJを積イデアルという。IJ＝{ax*by|x,y∈R}=(ab)だから、(a)(b)=(ab) （例) 整数環ZのイデアルA=(6),B=(9)から、AB={6x9y|x,y∈Z} = (54) ＜イデアルの重なり＞ I∩Jを交わり？イデアルという。a,bの最小公倍元をLとすると、I∩J＝{Lx|x∈R}=(L) (a)∩(b)=(L(a,b)) （例）整数環ZのイデアルA=(6),B=(9)から、A∩B={L(6,9)x|x∈Z} =(18) ＜自明、極大、素＞ また、環Rに対して、イチ、Rを自明なイデアルという。・要素a,bの積abがイデアルPに属するなら、要素a,bも属するようなイデアルPを素イデアルという。　(n)が素イデアルであることとｎが素数であることは同値。 （例）整数環ZのイデアルA=(6),B=(18)では、Z全体ではなく、BだってAを部分にもつからAは極大ではない。 4*9=36∈(6)だけど、4,9∈(6)ではないから、(6)は素イデアルではない。 4*8=32∈(2)で、4,8∈(2)だから、(2)は素イデアルだね。素イデアル自体を環全体としてしまえば、それは極大イデアルでもあり、素イデアルでもある。・M＝(m)が環Rの真部分のイデアルで、IがMを含む真のイデアルだとすると、　それはM＝Iに限るとき、　つまり、MとRの間の大きさのIがとれないような最大のイデアルMのことを　環Rの極大イデアルという。・極大イデアルは素イデアルになる。・(m)が極大イデアルであることと、R/(m)が体であることは同値だ。（例）ｐが素数ならFp=Z/(p)は体。このとき、(p)はZの極大イデアルだ。・ユークリッド環なら単項イデアル整域で、単項イデアル整域なら一意分解環だ。・Rが単項イデアル整域なら、０でない素イデアルは極大イデアルだ。ｐが素元ならR/(p)は体だ。（例） Zはユークリッド整域だから、単項イデアル整域。(3)は素イデアルだから、極大イデアルだね。３は素元だから、F3=Z/(3)は体になるね。

質問：ガウス整数を（1＋i)を法とする剰余類に分ける視覚化はどうしたらよいでしょうか。 たとえば、Pythonでは、 zp=1+iとするために、zp=complex(1,1)とかきます。 rg = [x for x in range(-10, 11)]と整数リストを作りましょう。ガウス格子点はLtc=[ p + q i for p in rg for q in rg]で作れます。　　Ltc = [ complex(p,q) for p in rg for q in rg]　と書きます。格子点にzpをかけた点集合がB=[ zp * x for x in Ltc]です。これを右に１平行移動した点がB1=[ x + 1 for x in B]です。 pythonも、juliaもｘ座標だけのリストとｙ座標だけのリストを対応する順に作ります。 x = [ c.real for c in Rs] y = [ c.imag for c in Rs] このRsに複素数の点集合を入れると、ガウス平面上にドットcharaを書くように関数show(Rs,chara)を作っておくと、使いまわしができますね。 [IN]python #=============================== import numpy as np import matplotlib.pyplot as plt zp=complex(1,1) rg = [x for x in range(-10, 11)] Ltc = [ complex(p,q) for p in rg for q in rg] B=[ zp *x for x in Ltc] B1=[ x + 1 for x in B] def show(Rs, chara): xs=[c.real for c in Rs] ys=[c.imag for c in Rs] plt.plot(xs,ys,chara) show(B,'*') show(B1,'+') [OUT]

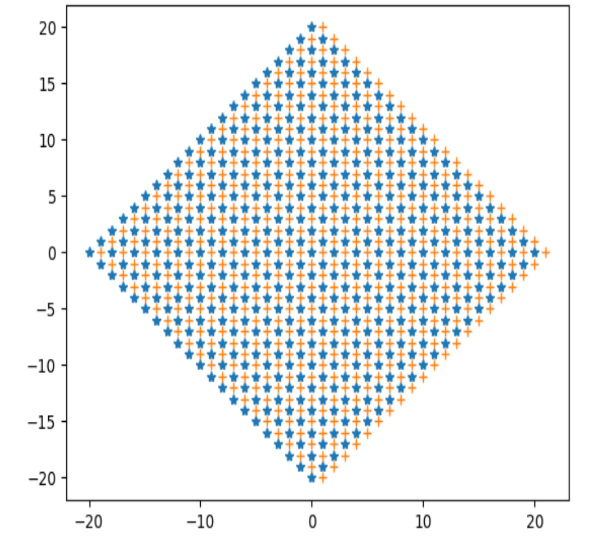
ガウス格子点の代わりに、アイゼンシュタイン格子点でも同じように剰余類が作れますね。関数型でかいたコードなので、geogebraの数式に移し替えやすいです。それが、このページの先頭のアプリです。

４．Z/(p)=Fpが体であることの具体的な確認

（例）F3 F３が体であることを具体で確かめておこう。 F3はZ/3Zだから、{0,1,2}の３要素でmod 3の剰余計算を含めた＋算と×算だ。＋算の０元はもちろん０だね。＋算の反元は0+0≡1+2≡0(mod 3)から、0,1,2のそれぞれ決まることがわかる。 ×算の１元はもちろん１だ。 ×算の逆元は1×1≡2×2≡1(mod 3)だから、1,2はそれ自身を逆元に持つことがわかる。だから、体になる。体なのだから、整域だし、ユークリッド整域であることは確実だけれど復習をかねて確認してみよう。ゼロ以外のｙでｘｙ≡０(mod 3)になるｘは０だけだから、ゼロ因子はないので、整域だ。 2÷1=2あまり０，1÷2=0あまり１。だから、わる数より小さな余りが決まるのでユークリッド整域だ。 （例）F５ F5が体であることを具体で確かめておこう。 F5はZ/5Zだから、{0,1,2,3,4}の5要素でmod 5の剰余計算を含めた＋算と×算だ。＋算の０元はもちろん０だね。＋算の反元は0+0≡1+4=2+3≡0(mod 5)から、0,1,2,3,4のそれぞれ決まることがわかる。 ×算の１元はもちろん１だ。 ×算の逆元は1×1≡2×3≡4×4≡1(mod 5)だから、1,2,3,4それぞれが逆元を持つことがわかる。だから、体になる。体なのだから、整域だし、ユークリッド整域であることは確実だけれど復習をかねて確認してみよう。ゼロ以外のｙでｘｙ≡０(mod 5)になるｘは０だけだから、ゼロ因子はないので、整域だ。 4÷2=2あまり0, 3÷2=1あまり1, 2÷2=1あまり0, 1÷2=0あまり1 4÷3=1あまり1, 3÷3=1あまり0, 2÷3=0あまり2, 1÷3=0あまり1, 4÷4=1あまり0, 3÷4=0あまり3, 2÷4=0あまり2, 1÷4=0あまり1, だから、わる数より小さな余りが決まるのでユークリッド整域だ。割り切れる場合は÷1以外では、4÷2=2, 2÷2, 3÷3,4÷4で。１とその数自身でしか割り切れない数は2,3だから素元は2,3。 4が合成元で4=2×2と素元分解できるね。