Función Lineal
- Definir y reconocer funciones lineales, en base a tablas de valores, de formulación algebraica y representación gráfica con el uso de la tecnología.
- Determinar las características de las representaciones de las funciones lineales.
- Elaborar conclusiones sobre la pendiente y la ordenada al origen de una función lineal.
- Reconocer la ecuación de la recta da la pendiente y un punto o dados dos puntos de la misma.
PARA EMPEZAR.....

Función Lineal - Material teórico y práctico
 Les propongo:
Les propongo:
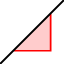
- Observar la división del desplazamiento vertical entre el desplazamiento horizontal.
- Comprobar que es igual la pendiente en el deslizador.

- Modificar la pendiente en el deslizador y ver cómo se comporta la recta: cuando es positiva, cuando es negativa y cuando es cero.
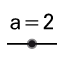
- Incrementar poco a poco el valor de la pendiente en el deslizador hasta llegar a 10 y concluir que para pendientes cada vez mayores la recta tiende a ser vertical.
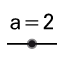
- Notar que el valor de llamado ordenada al origen sólo desplaza la recta de manera vertical y no influye en su inclinación.

- Mover los puntos C y D y observar que la pendiente no varía.

- Reflexionar acerca de la relación entre la pendiente y el ángulo de inclinación de la recta.
RESUMIENDO!!!!
 Aplicación de función lineal
Aplicación de función linealLa siguiente aplicación muestra el proceso de llenado de un tanque cuya capacidades de 10 litros mediante un grifo con flujo ajustable. Asigne los valores del flujo y volumen inicial de agua en el tanque. Utilice el los botones para controlar la animación. ¿Qué puede decirse acerca del flujo y el tiempo de llenado? ¿Qué representa en la gráfica? ¿Y el volumen inicial?
Ahora vamos a trabajar el concepto de pendiente con el siguiente ejercicio:
(Escribe tu respuesta en el recuadro)
 La pendiente es la inclinación de la recta con respecto al eje horizontal, también conocido como el eje de las abscisas. Esto significa que indica la cantidad en que se incrementa o disminuye el valor de la variable , cuando la aumenta una unidad. Se denota con la letra .
La pendiente es la inclinación de la recta con respecto al eje horizontal, también conocido como el eje de las abscisas. Esto significa que indica la cantidad en que se incrementa o disminuye el valor de la variable , cuando la aumenta una unidad. Se denota con la letra .
Determina el valor de "" de modo que la pendiente de la recta que pasa por los puntos y tenga el valor
En este video pueden ver la resolución del ejercicio anterior
MANOS A LA OBRA
 Ecuación de la recta que pasa por dos puntos
En el mapa de Europa que se puede encontrar en la parte inferior se encuentran representadas diferentes ciudades.
Despega un avión de Madrid con dirección a Moscú y queremos averiguar la ecuación de la recta que representa su trayectoria.
Averigua los parámetros "" y "" sabiendo que la forma de la recta es
Ecuación de la recta que pasa por dos puntos
En el mapa de Europa que se puede encontrar en la parte inferior se encuentran representadas diferentes ciudades.
Despega un avión de Madrid con dirección a Moscú y queremos averiguar la ecuación de la recta que representa su trayectoria.
Averigua los parámetros "" y "" sabiendo que la forma de la recta es ![[size=150][icon]/images/ggb/toolbar/mode_parallel.png[/icon]Dos rectas son [b]paralelas[/b] si sus pendientes son iguales.
[icon]/images/ggb/toolbar/mode_orthogonal.png[/icon]Dos rectas son [b]perpendiculares[/b] si sus pendientes son opuestas y recíprocas. [/size]](https://beta.geogebra.org/resource/vbhxzeky/wN6WRaxNNb7zMZFI/material-vbhxzeky.png)
 Dos rectas son paralelas si sus pendientes son iguales.
Dos rectas son paralelas si sus pendientes son iguales.
 Dos rectas son perpendiculares si sus pendientes son opuestas y recíprocas.
Dos rectas son perpendiculares si sus pendientes son opuestas y recíprocas.  Con esta APPLET podrán trabajar el concepto de rectas paralelas y perpendiculares.
Muevan los deslizaron para obtener una recta básica.
Elijan un punto y seleccionen paralela o perpendicular haciendo click en la casilla correspondiente
Con esta APPLET podrán trabajar el concepto de rectas paralelas y perpendiculares.
Muevan los deslizaron para obtener una recta básica.
Elijan un punto y seleccionen paralela o perpendicular haciendo click en la casilla correspondiente  y podrán obtener la ecuación de la recta
y podrán obtener la ecuación de la recta  o
o  a la recta básica que pasa por el punto seleccionado.
a la recta básica que pasa por el punto seleccionado. EJERCITAMOS UN POCO
A modo de cierre (Marca la opción correcta)
¿Cuál es el valor de a si (a,5) se encuentra en la recta 2x+y=9?
¿Cuál es la ordenada al origen de x+4y=12?
Corrobore sus respuesta graficando las funciones anteriores
La pendiente de r :
La función asociada a la gráfica de la imagen es:
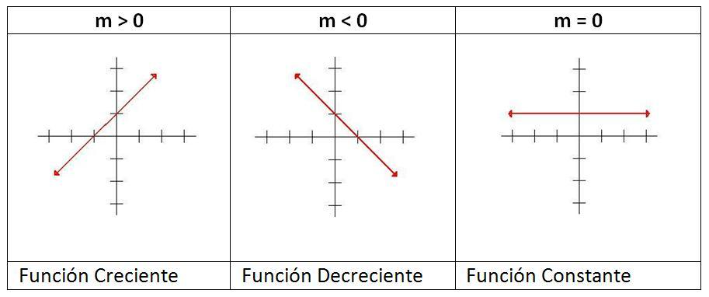
¿Cuál de las siguientes funciones es decreciente?
Analiza y responde:
Un andinista asciende un tramo de una montaña con una rapidez de 37 metros por hora.
Después de 4 horas ha llegado a una altura de 1.122 metros.
a) ¿Cuál es la función que indica la altura en metros después de x horas?
b) ¿A qué altura se encontraba cuando comenzó a escalar?
c) Grafique la función altura.
(Responde el recuadro de abajo)