半順序をhasseで図にしよう
1.文字列のハッセ図
このワークシートはMath by Codeの一部です。
ある数の約数を並べたときにその要素どうしに面白い関係性ができる。
この関係性は素因数分解を利用して約数の個数や約数の和を求めるときによく利用される。
それがハッセの図式だ。
たとえば、22*32*5=180をハッセ図で視覚化できる。
これがなかなかピンとこない子どもも多いので、
文字列のハッセ図をいろいろ見ることで、しくみを理解しやすくなったらうれしい。
<半順序集合>
たとえば、文字列”ab"の部分について考えてみよう。
A={a,b}の部分集合は{a,b},{a},{b},{ }の4つある。
BがAの部分であることをA≧Bという記号で表してみよう。
「部分である」という関係は3法則
反射、反対称、推移のどれも成り立つ。
つまり、
・AはAの部分、
・AがBの部分でBがAの部分ならA=B、
・AがBの部分でBがCの部分ならAはCの部分。
この3ルールに合格する関係性Rを半順序関係と呼ぶことにしよう。
特に反射が大切ですね。RにARAが成り立たないと「半順序だ」とはいいません。
「真部分である」A⊃Bではなく、A⊇Bの関係にしないと半順序にはなりません。
「真部分である」だと、推移しか成り立たないからです。
わりと見落としがちな、反射と反対称が大切なのですね。
このAの部分集合の集合S=2A=set({a,b},{a},{b},{ })の要素どうしで半順序チェックをしよう。
{a,b≧{a}≧{ }
{a,b}≧{b}≧{ }
2系統の「全順序関係(半順序で1直線に並ぶ、任意の2要素が半順序で比較できる)」が見つかった。
しかし、{a}と{b}には≧の関係はない。
比較できないので、全要素が全順序になるわけではないね。
だから、Sは全順序でない半順序集合と言われる。
つまり、半順序が一般で、全順序が特殊という言い方になるんだね。
質問:文字の集合Aの部分集合の集合S=2A。について、要素どうしが「部分である」関係を図で表すはどうしたらよいでしょうか。
半順序集合の2つの要素に半順序関係があるとき必ず線でつないでしまうと、
線が多くなって見づらくなる。
まず、反射律から、自分と半順序なので、どの要素にもループ辺できるが、これは不要だ。
また、推移律から、a,b,cがこの順で全順序になるときは、→が2本になったり、三角形ができてしまう。
これでは全順序が見づらいので、隣接する要素だけを線で結び、
全順序になる要素が連続する細分された辺はできるだけ直線にしよう。
ハッセは、これを単純に決めるために「直接大きい、直接小さい」という関係、
x≦yとなるx,yの間にx≦z≦yとなるzがない関係を線で結ぶとしている。
"a" が"ab"の直接小さい部分であるとき、a-abのように線でつなぐか、部分という順序がわかるように→をつけてみよう。
そうしてできるのがハッセの図式、図だ。
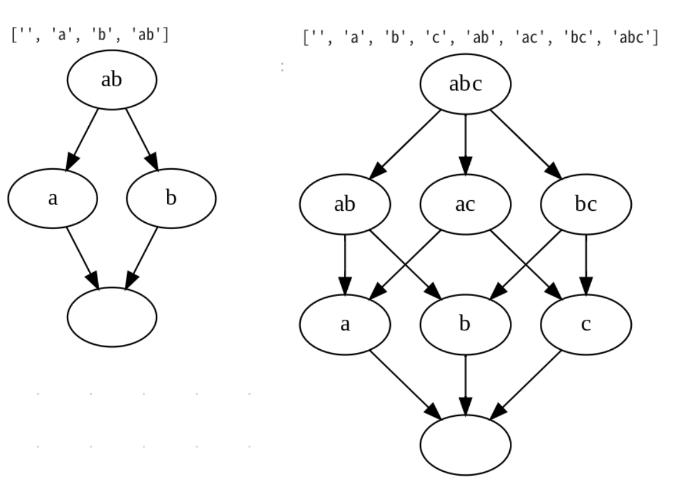
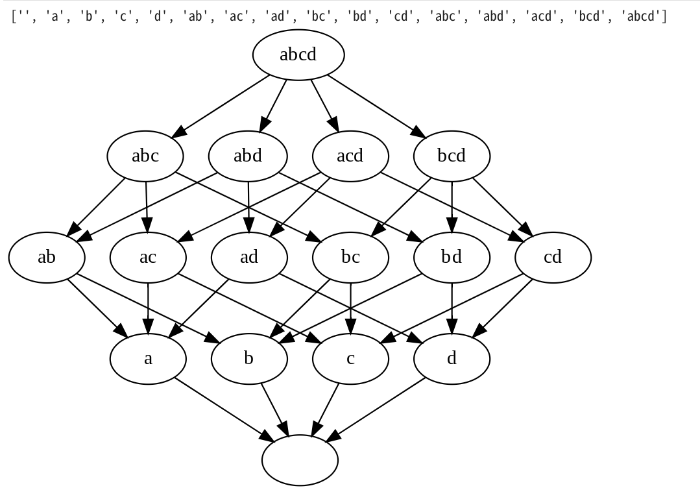
<ハッセ図をかくコード>
かなりきれいな図ができました。
質問:コードでハッセ図をかくにはどうすればよいでしょうか。
文字列から部分集合を作るのは、要素数を段階的に増やす方法があります。
全体の文字列itemsからcombinations(items.i)として、iを0からnまで増やして、
部分集合の集合nodesに追加してけば作れます。
ただ、combinationsを使うと、文字を取り出したリストができてしまいます。
ノードの名前にするためにjoinを使って、文字の間が空で連結し、文字列に直しましょう。
見かけ上は、部分集合というよりも部分文字列ということだね。
出来上がったnodesから2要素順序をつけて取り出します。permutations(nodes,2)を使います。
取り出した順にx,yとしたとき、
yがxより直接小さい部分集合なら、x→yの辺を作ります。
ただの部分集合ではなく、文字数が1違うという条件をつけて、直接小さい部分集合を選べますね。
図をかくためのパッケージはgraphvizを使いましょう。
networkxは相当指定を相当しないとハッセ図はかきにくいようです。
#=====================================
import graphviz
from itertools import permutations
def hasseG(items):
res=[]
n=len(items)
for i in range(n+1):
res =res + list(combinations(items,i))
nodes = [ ''.join(x) for x in res]
print(nodes)
G = graphviz.Digraph()
for pm in permutations(nodes,2):
x,y = pm
if set(y) <= set(x) and len(x) - len(y) == 1:
G.edge(x,y)
return G
#======================================
items="ab"
G = hasseG(items)
G
#======================================
items="abc"
G = hasseG(items)
G
#======================================
items="abcd"
G = hasseG(items)
G
#======================================
2。数のハッセ図
さっきは、文字列(文字の集合)の部分集合どうしのつながりを
ハッセ図で表しました。
いよいよ、数の半順序関係を視覚化することをやってみましょう。
まず、数の約数・倍数関係自体は静的なものです。
だから、状態変化はもともとありません。
そこで、できるだけ関数型プログラミングを考えて、ノードとそのつながりをさぐりましょう。
質問:数の約数からハッセ図を作るにはどうしたらよいでしょう。
・文字列のときと同じく、部分集合を作りnodesとする。
・nodesから2つ選び直接の大小関係なら→で結ぶ
この2段階でグラフデータを作りましょう。
まず入力した数をNとします。
Nの約数はN以下の数で割り切る数を集めるという宣言で作れます。それがnodesです。
次に、「直接小さい約数関係」を見つけるために、「2約数x,yについて
x÷yをやったときに余りがなく、商が素数であるという条件」を使いたい。
そこで、N未満の素数リストPを作りましょう。
nの約数個数を求める関数divCount(n)を作ります。nに対する約数mのリストの長さを返します。
2からN未満の数xにdivCount(x)をして、約数が2個の数を抜き出せば完了ですね。
ここまで準備できたら、文字列のときと同じように辺を作りましょう。
つまり、nodesから順番をつけて2つx,yを選び、それが直接小さい約数関係ならx→yします。
import graphviz
from itertools import permutations
def hasse(N):
#nodesは、Nの約数
nodes = list(filter(lambda m:N % m==0, list(range(1,N+1))))
#PはN未満の素数
M = list(range(2,N))
divCount = lambda n:len(list(filter(lambda m:n % m==0, list(range(1,n+1)))))
P = [x for x in M if divCount(x)==2]
print(nodes)
G = graphviz.Digraph()
for pm in permutations(nodes,2):
x,y = pm
if x % y ==0 and (x//y in P):
G.edge(str(x),str(y))
return G
#=====================================================
number=36
G = hasse(number)
G
#=====================================================
number=60
G = hasse(number)
G
#=====================================================
number=180
G = hasse(number)
G
#=====================================================
number=90
G = hasse(number)
G
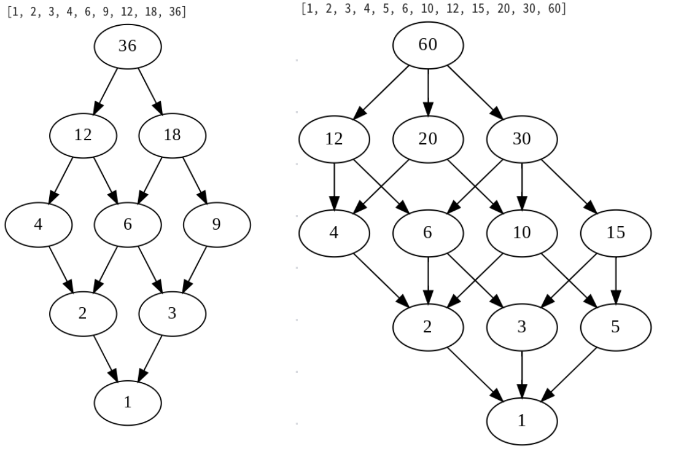
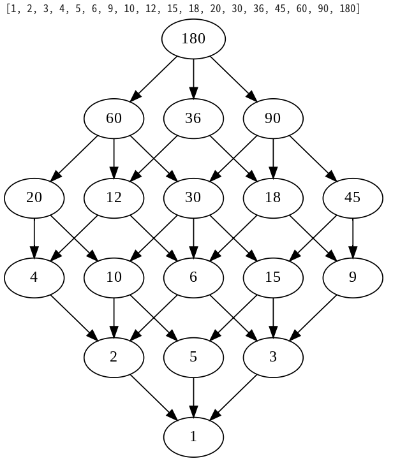
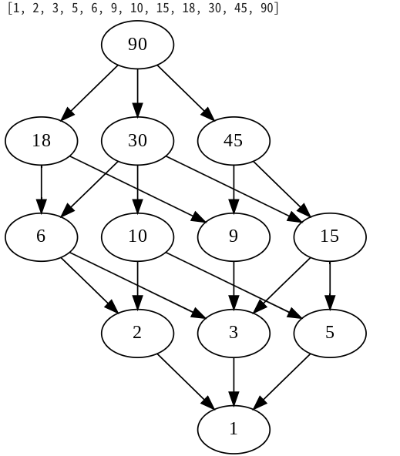
3。群のハッセ図
どうでしょうか。
180ではうまくいったのですが、90では少しきたないですね。
素数の種類を無視して積分解したときのかけ算の個数で
nodeの深さを決めているのかもしれません。
ハッセの図式は文字列、整数だけではなく、半順序関係があるときに使えます。
群・環・体の関係性を表すときにも使えます。応用が広そうですね。
たとえば、3要素の順列は6個ありますが、これを置換としてとらえなおして、
対称群S3という名前がついてます。
これは、
1→2→3→1のローテーション、順送り、いわゆる巡回置換ρ=(1 2 3)と
2↔3 の入れ替え、いわゆる互換τ=(2 3)を組み合わせて作ることができます。
S3はρを3回でもとにもどり、τを2回してももとにもどるので、単位元が作れます。
証明は省略しますが、S3は群になりますね。
S3の部分群は4種ありますね。
位数1のE={1}、
位数6のG={1,ρ,ρ2, τ,ρτ,ρ2τ},
位数3のR={1,ρ,ρ2}
位数2のA={1, τ}, B={1,ρτ},C={1, ρ2τ}
質問:このS3の部分群の関係を直接小さい部分関係でハッセ図にするにはどうしたらよいですか。
文字列や数のように、データから部分関係が判断できればよいのですが、
群の場合はそれがありません。基本は、そのまま指定することですね。
部分群の位数は群の位数の約数になりますが、
それは結果であって、十分な条件ではありません。
ただ、部分群の関係だとわかっている同士なら使えますね。
import graphviz
from itertools import permutations
def hasseG():
nodes = ["E","A","B","C","R","G"]
G = graphviz.Digraph()
G.edge("G","A")
G.edge("G","B")
G.edge("G","C")
G.edge("G","R")
G.edge("A","E")
G.edge("B","E")
G.edge("C","E")
G.edge("R","E")
return G
#=====================================================
G = hasseG()
G
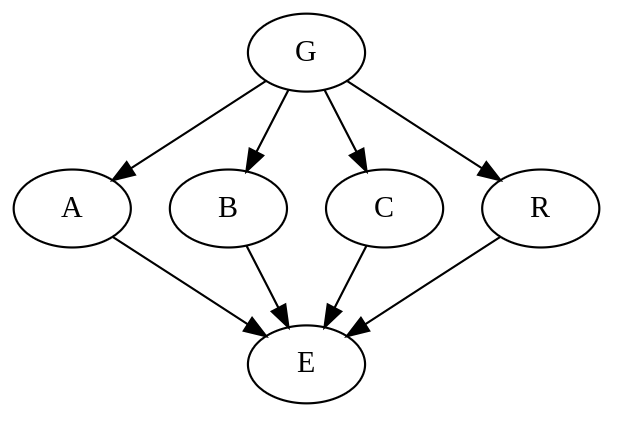
これではあまりに
単純すぎて、見た人がなにを表しているかがわかりません。
そこで、処理も表示も群らしく改良しましょう。
nodeはnameがキーでlabelが値の辞書で作り、Gに登録します。G.node(name=k, label=v)
・nameは、群の位数(要素数)がわかる文字列とします。
・labelは、表示のために群の要素の外延をそのまま表示しましょう。
そして、edgeには群の位数と位数の商(指数といいます)をつけます。
・この指数が素数であれば、直接の部分であると判断して辺とします。
(そうしないと、位数1の{1}が位数6のSの部分だということで→がつくことを避けたいからです。)
・そしてGに、始点、終点、指数を登録します。G.edge(str(x),str(y),str(div))
#===========================================================
import graphviz
from itertools import permutations
def hasseG(items):
G = graphviz.Digraph()
for k, v in items.items():
G.node(name = k, label =v )
nodes = items.keys()
#Pはitemsの位数以下の素数
M = list(range(2,len(items)))
divCount = lambda n:len(list(filter(lambda m:n % m==0, list(range(1,n+1)))))
P = [x for x in M if divCount(x)==2]
for pm in permutations(nodes,2):
x,y = pm
div = len(x)//len(y)
if len(x) % len(y) ==0 and (div in P):
G.edge(x,y,str(div))
return G
return G
#=====================================================
items={
"1":"{1}","1a":"{1,τ}","1b":"{1,ρτ}","1c":"{1,ρ^2τ}","1de":"{1,ρ,ρ^2}", "1abcde":"{1,ρ,ρ^2, τ,ρτ,ρ^2τ}"
}
G = hasseG(items)
G
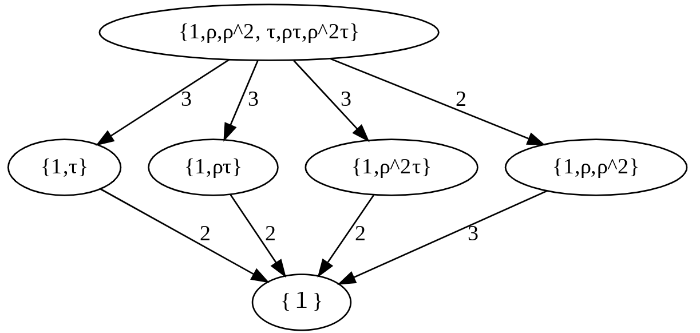
Latex表示などができるともっといいのですが、きりがないので、
このくらいにしておきましょう。