Clasificación de triángulos
Clasificación de los triángulos (en la geometría euclidiana) utilizando la relación de congruencia
¿Igualdad o congruencia?
La adopción indistinta de los términos “igualdad” y “congruencia” es una síntesis cargada de susceptibilidades que enmascarara una falta de toma de decisión hacia afuera, reñida (muchas veces) con íntimas convicciones de docentes que intentan eludir una de las tragedias de la educación matemática: la contradicción. Nos referimos aquí a las relaciones entre figuras geométricas en la educación de nivel medio. Hay educadores que eligen utilizar la relación de igualdad esgrimiendo necesidades acuciantes de facilitación didáctica, estamos quienes preferimos la congruencia ponderando las ventajas del lenguaje conjuntista y las relaciones funcionales, y, finalmente, están los que presentan ambos términos como sinónimos, en un probable intento abarcador que muestra tanto la imposibilidad de evadir esta discusión como la decisión de minimizar su importancia. Una forma adecuada de presentar la clasificación de triángulos utilizando la relación de congruencia podría incluir los siguientes tres ítems:
1) Propiedad de los ángulos del triángulo En todo triángulo la suma de sus ángulos es congruente con un ángulo llano.
2) Clasificación de los triángulos según sus lados Triángulos equiláteros: son los que tienen sus tres lados congruentes. Triángulos isósceles: son los que tienen dos de sus lados congruentes. Triángulos escalenos: son los que tienen sus tres lados no congruentes.
3) Clasificación de los triángulos según sus ángulos Triángulos acutángulos: son los que tienen sus tres ángulos agudos. Triángulos obtusángulos: son los que tienen un ángulo obtuso. Triángulos rectángulos: son los que tienen un ángulo recto.
La utilización del lenguaje conjuntista y sus relaciones, sugiere la no adopción de la terminología “ángulos interiores de un triángulo”, considerando que la noción intuitiva de “interior” está naturalmente asociada a la de “inclusión”, dentro y fuera del ámbito matemático. En todo caso, es el triángulo el que está incluido en cada uno de sus ángulos -tomando a estos como región del plano limitada por sus lados- o el que tiene a dos lados incluidos en los lados de cada ángulo -definiendo a los ángulos como pares de semirrectas del mismo origen-.
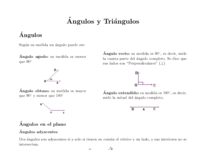
Ángulos y triángulos
Uno de los trabajos hallados en la web en los que se utiliza la relación de congruencia de una manera que consideramos apropiada, es el que presentamos al final y fue recuperado el 31/07/2018 en:
http://dme.ufro.cl/propedeutico/images/documents/clases/Clase%2010%20Angulos_Triangulos_ok.pdf
No coincidimos con algunas de las definiciones de dicho trabajo (como la de Triángulos), ni con la caracterización de ángulos "interiores" de un triángulo, pero valoramos muy positivamente el empleo de la medida y su relación con la congruencia.
Classificando triángulos
En el Décimo Segundo Congreso Argentino de Educación Matemática (15, 16 y 17 de septiembre de 2016 – Buenos Aires – Argentina), Claudia Lisete Oliveira Groenwald, de la Universidade Luterana do Brasil – ULBRA – Brasil (claudiag1959@yahoo.com.br) presentó, entre otros, el trabajo de GeoGebra que adjuntamos a continuación, titulado Classificando triángulos, como parte de su conferencia TECNOLOGIAS DA INFORMAÇÃO E COMUNICAÇÃO NO CURRÍCULO DE MATEMÁTICA.