La Funzione Integrale: definizione e proprietà
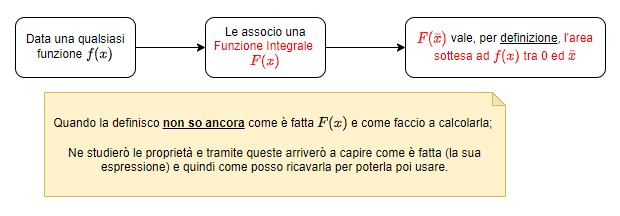
Per risolvere il problema dell'area sottesa al grafico di una funzione, introduciamo il concetto di Funzione Integrale: ad una qualsiasi funzione associamo una Funzione Integrale , che solitamente è indicata con la corrispondente lettera maiuscola.
Il risultato della Funzione Integrale per un qualsiasi valore di input è la misura dell'area sottesa ad tra e .
![Data una qualsiasi funzione [math]\textcolor{#007700}{y=f(x)}[/math] , definisco sua Funzione Integrale una funzione [math]\textcolor{red}{F(x)}[/math] che ad ogni valore di input [math]\bar{x}[/math] mi fornisce come risultato [color=#ff0000]l'area sottesa ad [math]\textcolor{#007700}{f(x)}[/math] tra [math]0[/math] e [math]\bar{x}[/math][/color].](https://beta.geogebra.org/resource/jkwwvscm/deTRa0gxb6w3b23h/material-jkwwvscm.png)
È chiaro che fino ad ora non abbiamo risolto il problema ma l'abbiamo solo spostato, perché non abbiamo ancora idea di come sia fatta la Funzione Integrale. Studiandone le proprietà, tuttavia, capiremo come si comporta e quindi impareremo come si fa a ottenerla.
LE PROPRIETÀ DELLA FUNZIONE INTEGRALE
Vediamo alcune proprietà della Funzione Integrale, che possiamo dedurre dalla sua definizione senza sapere esattamente come è fatta. Ci accontenteremo di "giustificare" queste proprietà, senza dimostrarle, perché esse appaiono piuttosto "verosimili" e dirette conseguenze della definizione.
LINEARITÀ DELLA FUNZIONE INTEGRALE
La Funzione Integrale gode delle proprietà di linearità, cioè
1a) Moltiplicando una funzione per una costante, i risultati della corrispondente Funzione Integrale si ottengono moltiplicando per la stessa costante quelli della Funzione Integrale originale.
Il concetto può anche essere formulato nel seguente modo, che chiarisce come al solito la costante si possa "portare fuori":
La giustificazione di questa proprietà è abbastanza immediata: se moltiplico per una costante una funzione, significa che tutti i suoi risultati, cioè le "altezze" dei rettangolini con cui calcolerò l'area, verranno moltiplicati per quella costante. Di conseguenza l'intera area verrà modificata allo stesso modo.
![La funzione [math]\textcolor{blue}{y=g(x)}[/math], si ottiene moltiplicando [math]\textcolor{red}{y=f(x)}[/math] per [math]3[/math], di conseguenza in ogni punto sarà "tre volte più alta": ne consegue anche anche l'area sottesa, definita dalla sua Funzione Integrale, darà risultati tripli.](https://beta.geogebra.org/resource/ajtycxd3/8gV3PPXSKRltXjA8/material-ajtycxd3.png)
1b) La Funzione Integrale di una somma di due funzioni è la somma delle corrispondenti Funzioni Integrali.
Il concetto può anche essere formulato nel seguente modo, che mostra come anche l'integrale definito si possa "spezzare" nella somma di due integrali, allo stesso modo di quello indefinito:
Anche la giustificazione di questa proprietà è abbastanza intuitiva: se sommo due funzioni, ottengo una funzione che in ogni punto ha un'"altezza" che è pari all'altezza delle due funzioi originali, quindi anche la corrispondenti aree staranno nella stessa relazione.
![In ogni punto il risultato della funzione [math]\textcolor{orange}{h(x)}[/math] è la somma dei risultati di [math]\textcolor{red}{f(x)}[/math] e [math]\textcolor{blue}{g(x)}[/math].
Verrà quindi approssimata da rettangolini le cui altezze sono la somma delle corrispondenti altezze dei rettangolini utilizzati per le altre due funzioni, da cui si può dedurre che anche l'area complessiva sotto ad [math]\textcolor{orange}{h(x)}[/math], definita dalla sua Funzione Integrale, può essere ottenuta come somma delle altre due.](https://beta.geogebra.org/resource/mr3e4gcw/blgEAzwraD7hDI7N/material-mr3e4gcw.png)
ALTRE PROPRIETÀ DELLA FUNZIONE INTEGRALE 2) Il calcolo dell'area può essere spezzato in più contributi lungo l'intervallo di calcolo. la giustificazione di questa proprietà è abbastanza immediata, e si può vedere nella figura sotto.![È abbastanza evidente che l'area sottesa alla funzione [math]f(x)[/math] nel tratto tra [math]0[/math] e [math]\bar{x}[/math] può essere vista come la somma delle aree relative a due tratti parziali.](https://beta.geogebra.org/resource/t7jvwhen/1Mymkn036Z01lq06/material-t7jvwhen.png)
Questa proprietà può essere espressa in un altro modo che ci sarà molto utile in seguito
Supponiamo di voler calcolare l'area sottesa ad una funzione in un intervallo , cioè . Invertendo la relazione appena trovata abbiamo
I due termini a secondo membro possono essere espressi, per definizione, tramite la Funzione Integrale, e quindi abbiamo
Ovvero
2a) l'area sottesa ad un certo intervallo può essere calcolata come differenza tra i valori assunti dalla Funzione Integrale agli estremi dell'intervallo stesso.
![[color=#38761d]L'area sottesa ad [math]f(x)[/math] tra [math]\textcolor{blue}{a}[/math] ed [math]\textcolor{#007700}{\bar{x}}[/math] [/color]può essere ottenuta considerando [color=#cc0000]quella tra [math]0[/math] ed [math]\textcolor{#007700}{\bar{x}}[/math][/color] e sottraendole [color=#0000ff]quella tra [math]0[/math] ed [math]\textcolor{blue}{a}[/math][/color].
Queste ultime possono poi essere espresse tramite la Funzione Integrale [math]F(x)[/math].](https://beta.geogebra.org/resource/cn2a9btp/wSykPEtytqgY6wdH/material-cn2a9btp.png)
3) Area sottesa ad un intervallo nullo.
Anche in questo caso la giustificazione è piuttosto intuitiva, dato che corrisponde all'area di un rettangolo a base nulla.