APS Geometry Unit 5 Book

MGSE9-12.G.C.1 Understand that all circles are similar. MGSE9-12.G.C.2 Identify and describe relationships among inscribed angles, radii, chords, tangents, and secants. Include the relationship between central, inscribed, and circumscribed angles; inscribed angles on a diameter are right angles; the radius of a circle is perpendicular to the tangent where the radius intersects the circle. MGSE9-12.G.C.3 Construct the inscribed and circumscribed circles of a triangle, and prove properties of angles for a quadrilateral inscribed in a circle. MGSE9-12.G.C.4 Construct a tangent line from a point outside a given circle to the circle. MGSE9-12.G.C.5 Derive using similarity the fact that the length of the arc intercepted by an angle is proportional to the radius, and define the radian measure of the angle as the constant of proportionality; derive the formula for the area of a sector. MGSE9-12.G.GMD.1 Give informal arguments for geometric formulas. a. Give informal arguments for the formulas of the circumference of a circle and area of a circle using dissection arguments and informal limit arguments. b. Give informal arguments for the formula of the volume of a cylinder, pyramid, and cone using Cavalieri’s principle. MGSE9-12.G.GMD.2 Give an informal argument using Cavalieri’s principle for the formulas for the volume of a sphere and other solid figures. MGSE9-12.G.GMD.3 Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems. Visualize relationships between two-dimensional and three-dimensional objects MGSE9-12.G.GMD.4 Identify the shapes of two-dimensional cross-sections of three-dimensional objects generated by rotations of two-dimensional objects.

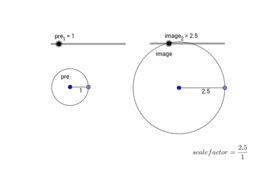
APS Geometry Unit 5 Book

Tabla de contenidos

MGSE9-12.G.C.1

MGSE9-12.G.C.2

MGSE9-12.G.C.3

MGSE9-12.G.C.4

MGSE9-12.G.C.5

MGSE9-12.G.GMD.1

MGSE9-12.G.GMD.3

Nuevos recursos

Descubrir recursos

Descubre temas