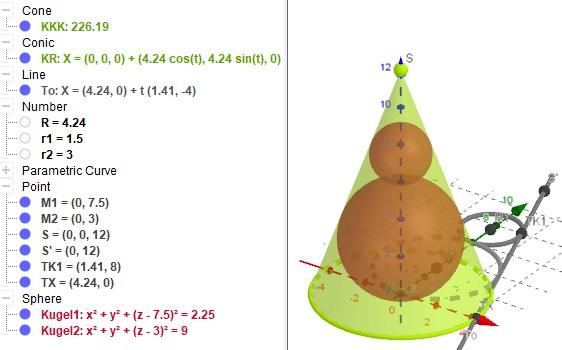
Tangente an zwei Kreise (zwei Kugeln im Kegel)
Konstruktion einer Tangente an 2 Kreise
In der App beschreibe ich die Kreise K1(M1,r1) und K2(M2,r2) mit Parametergleichungen
und lege die Tangentenpunkte (gleicher Winkel t) fest als K1(t), K2(t) die eine Tangenten-Gerade
bilden die mit der y-Achse geschnitten die Spitze S ergibt. Über den Thaleskreis über S,M1 erhalten ich den Tangentenpunkt TK1 für K1. Die Gerade S, TK1 geschnitten mit der x-Achse ergibt TX und damit den Radius R des Grundflächenkreises des Kegels.
Im Video verwende ich den Kreis mit dem Differenzradius aus r2, r1
um die Tangente von M1 an K3 zu bestimmen. Die Tangente verschiebe ich anschließend auf K1,K2 und die Schnittpunkte mit den Achsen ergeben S, TX zur Bestimmung des Kegels.
Kegel2einbeschriebeneKugelnCAS.ggb
Kegel2einbeschriebeneKugeln.ggb