Mel Buchner. Meditación sobre el Teorema de Pitágoras.
Mel Bochner (1940-2025) es uno de los fundadores del conceptualismo, arte en el que los conceptos y las ideas involucradas en la obra son priorizados sobre la estética o los materiales.
Gran parte de su obra tiene relación con las matemáticas, entre ellas están diversas versiones de Meditación sobre el teorema de Pitágoras que vemos en dos de sus representaciones: con avellanas (1972) o con cristales

La obra refleja la terna pitagórica (3,4,5) e intenta representar la idea de que 32*42=52 y en la versión izquierda lo hace sobre un triángulo rectángulo dibujado con tiza en el suelo.
El siguiente applet de GeoGebra utiliza la representación 3D para jugar con el resultado de que la suma de los dos cuadrados de la retícula de avellanas construidos sobre los catetos es igual al cuadrado del construido sobre la hipotenusa.
Encontramos una contradicción a la hora de aplicar el teorema de Pitágoras ya que, si el triángulo es rectángulo, las piezas colocadas sobre los vértices y los lados dividen en 2, 3 y 4 partes iguales, pero las distancias entre las avellanas de cada lado son distintas. Podemos hacer cálculos en una construcción de GeoGebra, en la que hemos situado el triángulo rectángulo sobre una imagen de la obra.
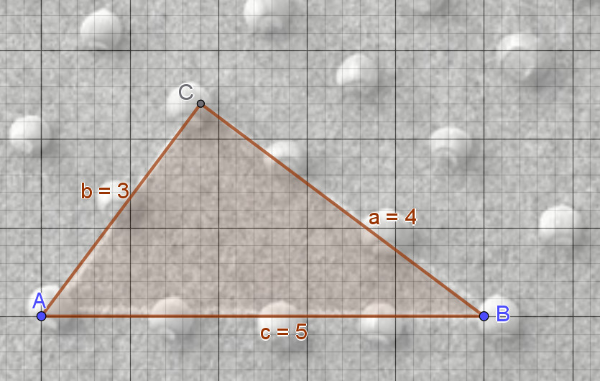
Las distancias entre los centros de las avellanas de la hipotenusa c sería 5/4=1.25, el el cateto b sería 4/3=1.33 y en el cateto a 3/2=1.5, por lo que en los catetos las medidas son un 6.4% y un 20% más grandes que en la hipotenusa.
Segunda aproximación al Teorema de Pitágoras
Se ha realizado una nueva construcción de GeoGebra que nos permita acercarnos más a la literalidad del
Teorema de Pitágoras. Reconstruimos la Meditación de Buchner con unos pocos cambios: llevamos las avellanas o los cristales a los puntos medios de los cuadrados situados en los lados del triángulo de forma que la terna (3,4,5) se corresponda con las medidas de los catetos y la hipotenusa del triángulo rectángulo.
Bibliografía
Arte conceptual en Wikipedia https://en.wikipedia.org/wiki/Conceptual_art
Raúl Ibáñez. Cultura pitagórica: arte. Cuaderno de cultura científica https://culturacientifica.com/2013/05/22/cultura-pitagorica-arte/