M1-Démarche expérimentale en mathématiques
ACTIVITE 1: Analyser une démarche expérimentale
1-Questionner
Expérimentez et identifiez les principaux questionnements mathématiques que soulèvent cette situation. Proposez des questions à destination des élèves pour les engager dans une démarche expérimentale.
2-Conjecturer
Expérimentez et formulez des conjectures mathématiques
3- Accompagner et structurer le raisonnement
a) Démontrez la conjecture principale et rédigez soigneusement votre réponse.
3-Accompagner et structurer le raisonnement
b) Identifiez les différentes étapes de la preuve et proposez des accompagnements possibles à destination des élèves
3-Accompagner et structurer le raisonnement
c) Démontrez chacune des autres conjectures, explicitez uniquement les propriétés mathématiques utiles à leur démonstration
3-Accompagner et structurer le raisonnement
d) Répertoriez les différents types de traces écrites produites par les élèves au cours de cette activité.
4- Accompagner la démarche expérimentale
Quels sont les apports de l'outil numérique dans la démarche expérimentale ?
ACTIVITE 2: A vous de jouer !
Situation 1: Volume d'une boite
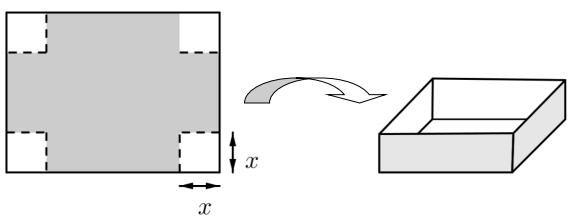
Quelle sera la valeur de x permettant d'obtenir une boite de volume maximal ?
SITUATION 2: Jeux de lumières

- A la première étape, on agit sur tous les interrupteurs allumant ainsi toutes les lampes.
- A la deuxième étape on n’agit que sur les interrupteurs dont le numéro est un multiple de 2, éteignant ainsi une partie des lampes.
- A la troisième étape on n’agit que sur les interrupteurs dont le numéro est un multiple de 3,etc...
SITUATION 3: Cagnotte
