Contenu
Die Sinuskurve
Sinuskurven sind für das berufliche und alltägliche Leben sehr wichtig, da sie in vielen wissenschaftlichen Breichen auftauchen. Man sollte zumindest mal gehört haben, was sie ist, wie sie ausschaut und wofür sie wichtig und brauchbar ist. Aber auch die Funktion von Kosinus und Tangens hängt mit dem Sinus und der Sinuskurve zusammen. Der mathematische Begriff für diesen Zusammenhang und diese Art von Funktionen nennt man Trigonometrie. Sinus, Kosinus und Tangens sind ganz normale Werte mit denen man rechnen kann und die auch auf den meisten Taschenrechnern zu finden sind. Der Sinus ist in einem rechtwinkligen Dreieck beispielsweise das Ergebnis aus der Gegenkathete eines Winkels durch die Hypothenuse, der Kosinus das Ergebnis von Ankathete durch Hypothenuse und der Tangens das Ergebnis von Gegenkathete durch Ankathete.
Allerdings beschäftigt sich das Buch hier ausschließlich mit der Sinus-Funktion und seiner graphischen Darstellung, die auch Sinuskurve genannt wird wegen ihrer Form.
Die Sinus-Funktion findet auch seinen Gebrauch in der Physik und in der Musik beispielsweise. Sie kann verschiedene Formen annehmen und verschieden verwendet werden. Also achtet genau auf seine Eigenschaften, schaut euch alles aufmerksam an und habt Spaß dabei und lernt hoffentlich was neues.
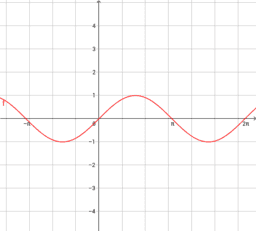
Die Normale Sinus-Funktion
Die normale einfachste Form der Sinus-Kurve hat die Funktion: f(x): sinx Es hat eine Periodenlänge von "2Pi", hat eine Amplitude von 1, hat seine Wertemenge von (-1;1) und seinen Ursprung bei (0/0). Der Graph einer solchen Funktion wird in diesem Kapiltel dargestellt und genau anlysiert.