Vergrotingsfactor - Mavo 2
Vergrotingsfactor uitrekenen
De vergrotingsfactor reken je uit door de lengte van het beeld te delen door de lengte van het origineel.
Vergrotingsfactor = lengte beeld : lengte origineel
Het origineel is het figuur waar je mee begint en na de vergroting/verkleining hou je het beeld over.
In deze opdracht is het origineel de driehoek ABC en het beeld is de driehoek A'B'C'
1. Reken de vergrotingsfactor uit.
2. Controleer of de vergrotingsfactor klopt door het vakje aan te klikken.
3. Reken de lengte van de onbekende zijde uit.
4. Controleer of de lengte van de zijde klopt door het vakje van de goed kleur aan te klikken.
Je kan zo vaak blijven oefenen als je wil. Als je op de knop 'nieuwe driehoek' klikt komt er een nieuwe vergroting of verkleining.
Van vergrotingsfactor naar oppervlakte
Je hebt hier boven geoefend met het uitrekenen van de vergrotingsfactor.
Nu kunnen we ook kijken hoe groot de oppervlakte van het beeld wordt.
In de onderstaande plaatje kun je zien hoe vaak het origineel in het beeld past door hokjes te tellen.
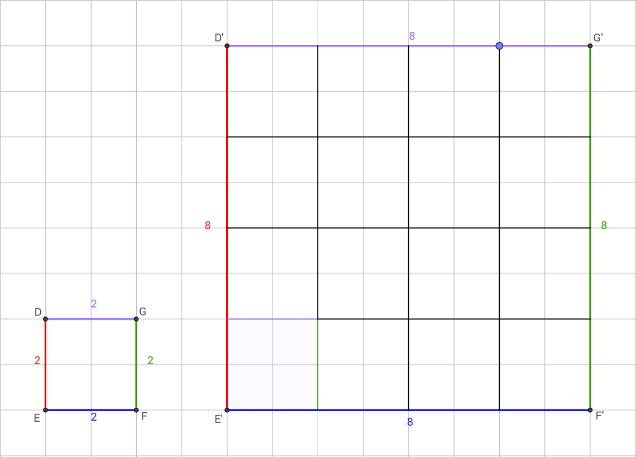
De vergrotingsfactor in dit plaatje is 8 : 2=4
We kunnen zien dat de oppervlakte van deze vergroting 64 hokjes is.
De oppervlakte van het origineel is 4 hokjes.
De oppervlakte is dus 64 : 4= 16 keer zo groot geworden. (het origineel pas 16 keer in het beeld)
De vergrotingsfactor = 4
De oppervlakte is 16 keer groter geworden, dat is hetzelfde als 42
Oppervlakte beeld = vergrotingsfactor2 x oppervlakte origineel
Oefenen met vergroten van oppervlakte
1. Reken de vergrotingsfactor uit.
2. Controleer of de vergrotingsfactor klopt door het vakje aan te klikken.
3. Reken de oppervlakte van het beeld uit door de vergrotingsfactor te gebruiken.
4. Controleer of de berekening en het antwoord kloppen door het vakje 'oppervlakte beeld' aan te klikken.
Je kan zo vaak blijven oefenen als je wil. Als je op de knop 'nieuw vierkant' klikt komt er een nieuwe vergroting of verkleining.
Van vergrotingsfactor naar inhoud
Je hebt hier boven geoefend met het uitrekenen van de oppervlakte van een vergroting.
Nu kunnen we ook kijken hoe groot de inhoud vaneen vergroting wordt.
In de onderstaande plaatje kun je zien hoe vaak het origineel in het beeld past door de schuifknoppen te gebruiken en daarna het aantal kubussen te tellen.
Je zult zien dat de inhoud van het origineel altijd keer de vergrotingsfactor tot de macht 3 gedaan moet worden om de inhoud van het beeld te krijgen.
Inhoud beeld = vergrotingsfactor3 x inhoud origineel
1. Reken de vergrotingsfactor uit.
2. Controleer of de vergrotingsfactor klopt door het vakje aan te klikken.
3. Vul de grote kubus met kleine kubussen door de gekleurde schuifknoppen te gebruiken.
4. Reken de inhoud van het beeld uit door de vergrotingsfactor te gebruiken.
5. Controleer of de berekening en het antwoord kloppen door het vakje 'inhoud beeld' aan te klikken.
Je kan zo vaak blijven oefenen als je wil. Als je op de knop 'nieuwe kubus' klikt komt er een nieuwe vergroting.