Regular and star-heptagons
In a regular heptagon whose sides are unit long (see the figure), AH³-AH²-2AH+1=0 holds. But when we draw a star-heptagon (with the same construction steps), also the equation AH³+AH²-2AH-1=0 may hold.
On Wikipedia we can learn more on regular star-heptagons. Basically, there are two kinds of them: {7/2} and {7/3}, they are shown in blue and green in the figure below, respectively.
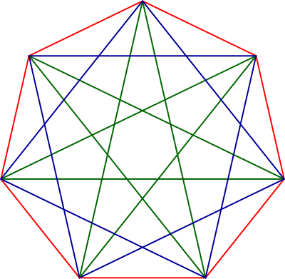
In {7/2} another theorem is valid, namely that (AI/AC)³+(AI/AC)²-2(AI/AC)-1=0.
If the length of the segment q(=AC) is considered to be 1, then the length of b(=AI) is the root of the polynomial x³ + x² - 2x - 1 = 0. When substituting x by (AI/AC), we obtain the above mentioned statement.
Note that the roots of x³ + x² - 2x - 1 are -1.80194..., -0.44504... and 1.24698... These numbers are the opposites of the roots of the polynomial x³ - x² - 2x + 1 = 0. The absolute values of these numbers contain the ratios between AH and BH(=1) and AI and AC, namely 1.80194... and 1.24698..., respectively. In fact, for {7/3} we need to obtain a similar result, but with the numerical value 0.44504... Since it is the root of x³ - x² - 2x + 1 = 0, we learn that for {7/3} a similar result is valid as for the regular (non-star) case, namely, we must consider the polynomial x³ - x² - 2x + 1 = 0 again.