Esboço
A gömbtől az elliptikus geometriáig
Ajánlás: Szabó József tanár úr emlékére
https://hu.wikipedia.org/wiki/Szab%C3%B3_J%C3%B3zsef_(matematikus)
Az euklideszi geometria - ezen belül az euklideszi szerkesztések - témakörén túllépve megismerkedhettek érdeklődő olvasóink a hiperbolikus geometria egy modelljével, kézhez kapták azt az eszköztárat, amellyel maguk is végezhetnek szerkesztéseket a P-modellen.
Ebben a GeoGebra Book-ban további két eszköztárat adunk érdeklődő látogatóink kezébe. Egyrészt a gömbi geometria eszköztárát, amely lehetővé teszi, hogy rajzolhassanak a gömbön. Másrészt az un. elliptikus síkgeometria modellezésére használható eszköztárat, amely szoros összefüggésben áll a gömbi geometriával.
Reméljük ezzel újabb ablakot sikerül nyitnunk jó néhány geometriai összefüggés minél alaposabb összehasonlító vizsgálatára.
Lista de conteúdos
A gömbi geometria
Az elliptikus geometria
- E 01 Az elliptikus síkgeometria gömb-modellje
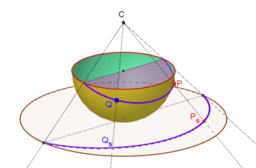
- E 02 Az Elliptikus sík félgömb-modellje
- E 03 Az elliptikus sikgeometria körmodellje
- E 04 Legyen adott az E-síkon ...
- E 05 Egybevágósági transzformációk az E-síkon
- E 06 Legyen adott egy háromszög ...
- E 07 Az E-háromszög nevezetes vonalai és pontjai
- E 08 Parketták
- E 09 Legyen adott négy pont ...
- E 10 Pentagramma mirificum az E-modellen