5-30-25 Constructions with GeoGebra Day 2
You will be completing more advanced constructions. It may be helpful to refer to the various properties of quadrilaterals.
*Additional tools have been provided to save time.
Midpoint or Center (under the point tool 
organizer )
*All four tools below are on a new organizer
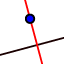Perpendicular Line
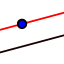Parallel Line
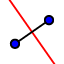Perpendicular Bisector
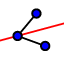Angle Bisector
Midpoint or Center (under the point tool organizer )
*All four tools below are on a new organizer
Perpendicular Line
Parallel Line
Perpendicular Bisector
Angle Bisector
Example 1, using the Midpoint Tool.
Construct the midpoint of segment AB by selecting the Midpoint or Center Tool 
. Then, select point A, followed by point B. The midpoint should appear in red.
*Hint, the midpoint or center tool is located under the point menu.
. Then, select point A, followed by point B. The midpoint should appear in red.
*Hint, the midpoint or center tool is located under the point menu.Example 2, using the Perpendicular Line tool.
Construct a line perpendicular to line r through point Z. Select the perpendicular line tool . Then, select line r followed by point Z.
. Then, select line r followed by point Z.
Example 3, using the Parallel Line tool.
Construct a line parallel to line m through point P.
Select the parallel line tool . Then, select line m, followed by point P.
. Then, select line m, followed by point P. Example 4, using the Perpendicular Bisector tool.
Construct a perpendicular bisector of segment CD. Select the perpendicular bisector tool . Then, select point C followed by point D.
. Then, select point C followed by point D.
Example 5, using the Angle Bisector Tool.
Bisect angle V. Construct a third point on angle V. Then, select the angle bisector tool . Finally, select 3 points that make up the angle in either a clockwise or counterclockwise fashion.
. Finally, select 3 points that make up the angle in either a clockwise or counterclockwise fashion.
1. Construct a circle through three points.
Construct a circle such that points X, Y, and Z are along the circumference of the circle.
*Hint, this uses the same process as finding the circumcenter of a triangle. Use the new toolbar to speed up the process.
2. Construct a 22.5 degree angle.
Construct an angle equal to 22.5 degrees.
*Hint, start by constructing a 90 degree angle using perpendicular lines.
3. Construct a parallelogram
When you have constructed your parallelogram, measure all four sides to make sure that opposite sides are congruent. Then, drag your shape around to see if it remains a parallelogram.
*Hint, a parallelogram has opposite sides that are parallel.
4. Construct a rhombus.
When you have constructed your rhombus, measure all four sides. Then, drag your points around and see if your shape remains a rhombus.
*Hint, all four sides of a rhombus are congruent.
5. Construct a rectangle.
When you have constructed your rectangle, measure all four sides and angles. Then, drag your points around and see if your shape remains a rectangle.
*Hint, a rectangle has consecutive sides that are perpendicular to each other.
6. Construct a kite.
*Hint, a kite has diagonals that are perpendicular to each other but only one diagonal is bisected.
7. Construct an isosceles trapezoid.
*Hint, an isosceles trapezoid has one pair of parallel sides and one pair of opposite sides that are congruent.