DISTRIBUCIÓN NORMAL DE PROBABILIDAD
ACTIVIDAD DIAGNÓSTICA
Para entender cabalmente el tema que estudiaremos, es muy importante tener presente los siguientes conocimientos que ya tenemos en nuestro archivo memorístico:
Recordemos que la probabilidad se representa por un número entre 0 y 1 inclusive, de tal manera que el 0 es la total nula probabilidad de que ocurra un evento y 1 es la seguridad total de que el evento sucederá.
donde P(x) es la probabilidad de que ocurra el evento x.
Además, la suma de todas las probabilidades de que ocurra el evento también es igual a 1.
La interpretación de ésta última fórmula es porque alguno de los eventos posibles necesariamente debe de suceder.
Otra cosa que debemos tener presente, es que en ésta distribución podemos visualizar el comportamiento probabilístico de variables aleatorias contínuas. Es decir, variables que no sólamente se cuentan, sino que también se miden, además que describen numéricamente un comportamiento de nuestro interés. O sea, son variables cuantitativas o cuantificables.
Ejemplos de éste tipo de variables son:
Las estaturas de los alumnos de un grupo, el peso de un producto, el volumen que puede contener un recipiente, etc.
DISTRIBUCIÓN NORMAL
Ésta distribución tiene importancia porque una gran cantidad de fenómenos naturales, sociales, científicos y antropológicos, entre otros, se ajustan a sus características.
Entre tales características, podemos mencionar:
- Su gráfica tiene forma de campana, por lo que también se conoce como Campana de Gauss o Distribución de Gauss, en honor de Karl Gauss.
- Por ser una distribución de probabilidad, el área bajo toda la curva es 1.
- La gráfica es asintótica con el eje de las abscisas (eje "x").
- Es simétrica respecto a la media . Además la media, moda y mediana tienen el mismo valor.
- La cantidad máxima de eventos, resultado esperado o mayor probabilidad de ocurrencia es la media
- La posición de la distribución en un plano cartesiano está determinada por la media .
- La dispersión de la distribución está determinada por la desviación estándar .
- Los puntos de inflexión donde cambia la curvatura de la distribución se encuentran en los puntos
- Bajo ésta distribución, podemos encontrar que el 68.3% de los eventos se encuentran dentro de ; el 95.4% de los eventos se encuentran dentro de y el 99.7% se encuentran dentro de . El 0.3% restante se debe a aberraciones o situaciones fuera de control.
Distribución normal o Campana de Gauss
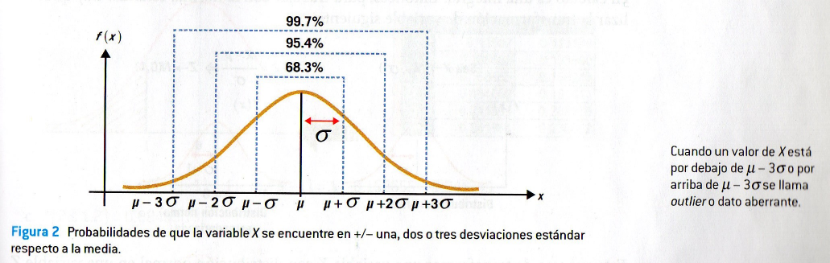
Es de notar que la campana de gauss está centrada en la media , tal y como indican las características descritas
Calcular las probabilidade de que suceda un rango de eventos es una tarea verdaderamente ardua, ya que hay que resolver una integral, pero gracias a dedicados matemáticos que han hecho por nosotros esa loable labor, podemos evitarnos ése trabajo y utilizar las tablas de valores que nos han que nos han legado.
Nosotros solamente debemos tomar los valores de la probabilidad correspondiente a la media y la desviación estándar que correspondan, resultando una forma bastante sencilla de utilizar.
Las tablas son las siguientes:
Tabla de Distribución Normal Acumulada


Se debe hacer notar que las tablas están estandarizadas para y , por lo que, para poder obtener probabilidades con otros valores, se debe hacer un cambio de la siguiente forma:
Sea el valor estandarizado y el valor que se desea calcular.
Entonces:
y ahora sí podemos recurrir a las tablas.
EJEMPLOS RESUELTOS
Hagamos un ejemplo para entender el uso de la tabla:
Supongamos que se tiene un proceso en el que el promedio es y la desviación estándar es
Calcular:
a) La probabilidad de obtener un resultado menor o igual a 2.5
b) La probabilidad de obtener un resultado mayor a -3.
c) La probabilidad de obtener un resultado menor o igual a 3.3
d) La probabilidad de obtener un resultado entre -2 y 2 inclusive.
SOLUCIÓN:
a)
Primero encontremos el valor de z que es de nuestro interés:
así que lo que vamos a calcular es toda el área bajo la Campana de Gauss hasta
Refiriéndonos a las tablas, buscamos en la columna de la izquierda el valor -0.2 y en el renglón superior el valor 0.05. En el cruce obtendremos la probabilidad que nos interesa:
de probabilidad.
b)
Calculamos el valor de z que nos interesa:
Pero la tabla muestra valores acumulados de z hasta el valor que buscamos, por lo que para valores mayores debemos encontrar
Así que buscamos en la tabla el valor de la probabilidad cuando . En la columna izquierda buscamos -3.0 y en el renglón superior buscamos 0.00 y en cruce encontraremos el valor buscado:
Por lo tanto:
de probabilidad
c)
Primero calculamos el valor de z que nos interesa:
Buscamos en la tabla el cruce de 0.1 y 0.05 para obtener la probabilidad solicitada:
de probabilidad.
d)
Ahora se nos pide un intervalo definido, por lo que debemos obtener un valor de z para cada uno de los límites que nos piden:
Para obtenemos
y para tenemos que
Buscamos en las tablas la probabilidad y y encontramos:
y
Por lo que nuestro resultado es:
Entonces, encontraremos la siguiente probabilidad:
de probabilidad.
La gráfica de el proceso descrito sería la siguiente. Puedes modificar los valores de x deseados y obtener la probabilidad para comparar con los resultados obtenidos:
SOLO PARA PRACTICAR
Una empresa que produce garrafones de pet para contener agua se le pide una corrida de recipientes con una capacidad de 4 lt. Sus estadísticos son los siguientes: capacidad promedio de los garrafones producidos lt con una variación lt. Calcular y graficar la Campana de Gauss del proceso:
a)
b)
c)
RESPUESTAS:
a) 84.13 %
b) 36.94 %
c) 8.74 %