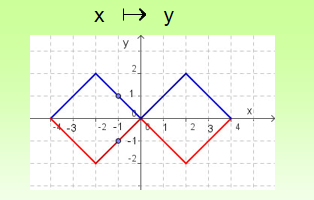
Pojam funkcije

Primjer 1.
Svakom učeniku možemo pridružiti njegov broj godina.
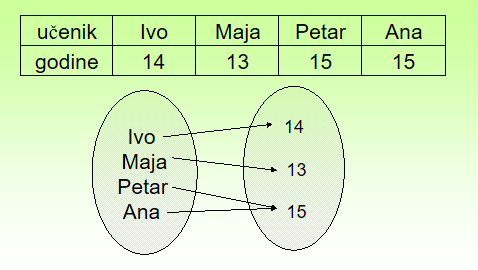
Primjer 2.
Učenicima u nekom razredu pridružujemo ocjene iz matematike
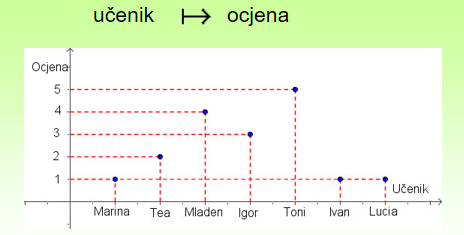
Kada se radi o pridruživanju brojeva, ono je najčešće zadano formulom,
koja potpuno određuje postupak pridruživanja. Međutim, sama formula nije dovoljna.
Primjer 3.
Formulom može se opisati više pridruživanja

Primjer 4.
Ako je tečaj 1 EUR = 7.3 kn, formula prikazuje odnos između eura i kune.
Izračunajmo neke vrijednosti:

FUNKCIJA je pridruživanje
(označimo ga s f) elemenata dvaju skupova po nekom zadanom pravilu, pri čemu
se svakom elementu x prvog skupa pridruži samo jedan element y drugog skupa.
Pišemo:
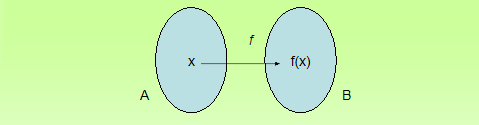
Skup A nazivamo područjem definicije ili domenom funkcije,
a skup B područjem vrijednosti ili kodomenom funkcije.
Riječ funkcija dolazi od latinske riječi functio što znači izvršenje, izvođenje.
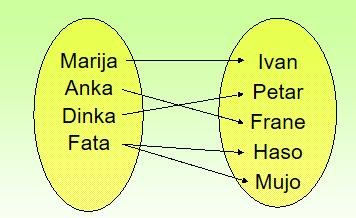
Primjer 5.
Ovo pridruživanje “moj suprug” nije funkcija jer Fata ima dva supruga.
Primjer 6.
Ovaj graf ne predstavlja grafički prikaz funkcije.
npr. broju x=-1 pridružena su dva broja: y=1 i y=-1.
Možeš li očitati još neke vrijednosti?