Paralaje
Intente mirar un objeto lejano solamente con el ojo izquierdo abierto y poner su dedo índice justo tapando el objeto. Cierre ahora el ojo izquierdo y abra el ojo derecho. ¿Observa la misma perspectiva? Este efecto es debido al paralaje.

En la imagen se puede ver la perspectiva que se obtiene colocando un dedo y mirando un objeto lejano. Primero, con el ojo derecho cerrado y el izquierdo abierto (imagen izquierda), y posteriormente el derecho abierto y el izquierdo cerrado (imagen derecha).
El paralaje es un fenómeno óptico que se produce cuando observamos un objeto desde dos puntos de vista diferentes.
Esto se debe a que cada ojo ve el objeto desde una posición ligeramente distinta. Cuando miramos un objeto con un solo ojo, no podemos apreciar su profundidad o su distancia con precisión, ya que no hay diferencia de perspectiva entre nuestros dos ojos. Pero al mirar con ambos ojos, nuestro cerebro puede comparar las dos imágenes y determinar la distancia y la profundidad de los objetos en nuestra vista.
El paralaje es el responsable de nuestra visión tridimensional, pero también se se puede utilizar este fenómeno para calcular distancias a objetos.
Paralaje en astronomía
El paralaje se utiliza en astronomía para determinar la distancia a estrellas y planetas. Los astrónomos toman mediciones de un objeto en el cielo desde diferentes ubicaciones en la Tierra en momentos diferentes, generalmente con un intervalo de seis meses. Estas mediciones se comparan para determinar el ángulo de paralaje, p, que es la diferencia angular en la posición aparente del objeto estelar.
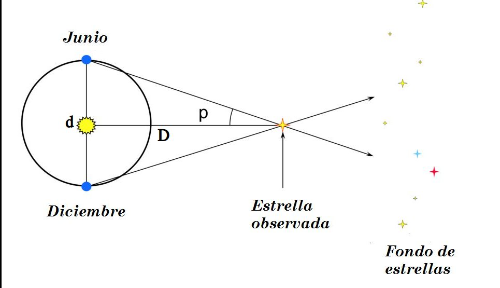
El triángulo formado por el objeto en el cielo y los dos puntos en la Tierra tiene una base conocida (la distancia entre los dos puntos de observación, por ejemplo en Junio y Diciembre) y un ángulo conocido (el ángulo de paralaje medido). Utilizando trigonometría, es posible determinar la distancia al objeto estelar mediante la resolución del triángulo. Si llamamos p al ángulo de paralaje, d a la mitad de la distancia entre las dos observaciones y D a la distancia al objeto entonces
tan p = d/D
de forma que que puede calcular D
D=d/tan p
En la siguiente hoja dinámica se calcula el valor de D para distintos valores de d y del ángulo. El deslizador controla la distancia base, es decir, d/2. De esta forma se puede modificar la distancia d con el deslizador, y también se puede desplazar el punto amarillo para obtener diferentes ángulos de paralaje, p.
Como la hoja tiene un objetivo ilustrativo, solamente usa un redondeo de dos decimales. Por eso los cambios en la distancia no se aprecian hasta que el ángulo o la distancia cambian significativamente.
Actividad 1
Manipule la hoja dinámica para, tomando una distancia base = 4, colocar un objeto tal que su ángulo de paralaje sea igual a 5 grados. ¿Cuál es la distancia D a la que se encuentra?
Actividad 2
Utilizar la hoja dinámica para calcular la distancia a un objeto cuyo ángulo de paralaje es 3.4 grados suponiendo una distancia base d=3
Actividad 3
¿Cuál sería la distancia D a un objeto tomando d=8 y p=9.16?