3.9 Centers of a Triangle - The Incenter
Problem 1
Kolton’s father installs sprinkling systems for farmers. Sometimes Kolton’s father has to install sprinkler systems on triangular-shaped pieces of land. He wants to be able to locate the “pivot point” (INCENTER) in the triangular field so the circle being watered will touch each of the three fences that form the boundaries of the field.
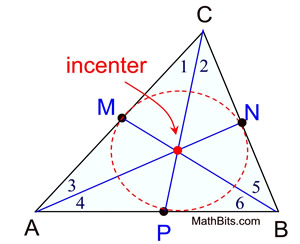Learn more about the incenter here.
Learn more about the incenter here.Learn the steps to find the Incenter and build the Incircle
Explore it on your own
Go to this website and explore how to find the INCENTER and build the INCIRCLE.
Learn how to find the INCENTER using GeoGebra
Find the INCENTER and build the INCIRCLE
What are the properties of the incenter?
What are the properties of the incircle?
Kolton’s Notes!
I constructed the angle bisectors of angle ACB and angle ABC. They intersected at point P, the INCENTER. So I wouldn’t get confused by so many lines in my diagram, I erased the rays that formed the angle bisectors past their point of intersection. I then drew ray AH through point P, the point of intersection of the two angle bisectors. My question is, “Does this ray bisect angle CAB?”
In order to prove that segment AH bisects FAG, we need to prove FAPGAP by demonstrating that triangles FAP and GAP are congruent.
In order to prove that segment AH bisects FAG, we need to prove FAPGAP by demonstrating that triangles FAP and GAP are congruent.Step 1
Segment AP is congruent to segment PA by
Step 2
Given that we built GP perpendicular to AB, then the angle AGP is a(n):
Step 3
Given that we built FP perpendicular to AC, then the angle AFP is also a
Step 4
Segments FP and PG are congruent because they are ___________ of the INCIRCLE.
Step 5
Therefore, triangles AFP and AGP are congruent by:
Step 6
Finally, we can state that angles FAP and GAP are congruent by
Reflection
After reviewing the incenter concept, complete Kolton’s argument in your own words.