Intervalos de concavidad
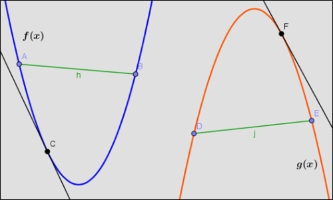
Desde una concepción visual, una curva convexa se asemeja a un valle mientras que una curva cóncava se asemeja a una montaña. Así las cosas, en la figura que se muestra más adelante, f(x) es una función convexa y g(x) es una función cóncava.
Función cóncava
Una función es cóncava cuando la recta tangente a la curva en cualquier punto de la función queda ubicada encima de la gráfica de la función. También, cuando el segmento que une a dos puntos de la función queda debajo de la gráfica.
Por lo tanto, la función g(x) de la figura es cóncava:
- F es un punto que pertenece a g(x). Independientemente de la posición de F, la recta tangente por ese punto siempre queda encima de la gráfica.
- D y E son dos puntos que pertenecen a g(x). El segmento j siempre queda dentro de la gráfica.
Función convexa
Una función es convexa cuando la recta tangente a la curva en cualquier punto de la función queda ubicada debajo de la gráfica de la función. También, cuando el segmento que une a dos puntos de la función queda encima de la gráfica.
Por lo tanto, la función f(x) de la figura es convexa:
- C es un punto que pertenece a f(x). La recta tangente por C siempre queda debajo de la gráfica.
- A y B son dos puntos que pertenecen a f(x). El segmento h siempre queda encima de la gráfica.
Puntos de inflexión
Puntos de inflexión son los puntos donde la función cambia de concavidad.
En el applet que se presenta a continuación, el criterio de concavidad se da utilizando la recta tangente a las 3 funciones que muestran.