Zentrische Streckung
Zentrische Streckungen sind wie Achsenspiegelungen, Punktspiegelungen, Drehungen und Verschiebungen geometrische Abbildungen. Auf diesem Arbeitsblatt
- lernst du die Definition der zentrischen Streckung kennen (1)
- machst du dich mit der Konstruktion von Bildfiguren vertraut (2)
- entdeckst du wichtige Eigenschaften der zentrischen Streckung (3).
(1) Definition der zentrischen Streckung
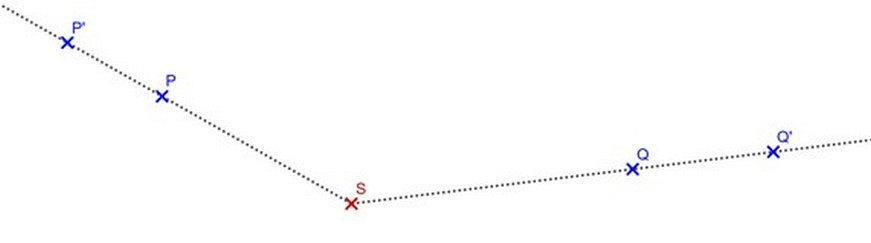
Der Bildpunkt P' eines Punktes P liegt auf derselben vom Streckzentrum S ausgehenden Halbgeraden (=Strahl) wie P. Der Abstand zu S wird mit dem (positiven) Streckfaktor k multipliziert: |SP'| = k * |SP|.
Im Bild ist k = 1,5.
Aufgabe 1
- Was ändert eine Vergrößerung / Verkleinerung des Streckfaktors an dem Bild?
- Welche Sonderfälle können bei der Wahl von positiven Streckfaktoren auftreten?
- In welche Bereiche kann man positive Streckfaktoren demnach aufteilen?
- Welche Abwandlung der Definition wäre für negative Streckfaktoren sinnvoll, wenn diese zugelassen werden sollen?
(2) Konstruktion von Bildfiguren
Man kann zentrische Streckungen mit Hilfe eines Gummibands durchführen: Um den Streckfaktor 2 zu erhalten, markiert man es z. B. in der Mitte. Ein Ende fixiert man im Punkt S, durchs andere Ende steckt man einen Stift P' und bewegt ihn so, dass die Markierung P genau die Punkte der ursprünglichen Figur abfährt. Der Stift zeichnet dann die Bildfigur.

Aufgabe 2
- Skizziere, wie im obigen Beispiel die Bildfigur liegen würde.
- Was ändert eine Vergrößerung / Verkleinerung des Streckfaktors an der Bildfigur?
- Wie muss man die Konstruktion mit Gummiband verändern, um größere / kleinere positive Streckfaktoren zu erhalten? Welche Grenze gibt es hierbei?
- Welche Bereiche kann man bei positiven Streckfaktoren bezüglich der Bildfiguren unterscheiden?
- Wie muss man die Konstruktion mit Gummiband verändern, um noch kleinere positive Streckfaktoren als oben zu erhalten?
(3) Eigenschaften der zentrischen Streckung
Im folgenden Applet kannst du die Konstruktion von Bildfiguren ausprobieren, indem du mit dem Schieberegler einen Vergrößerungs- oder Verkleinerungsfaktor einstellst, den Punkt S an die gewünschte Stelle ziehst, den Stift einschaltest und dann die Markierung P am vorgegebenen Dreieck entlangziehst. Der Stift P' zeichnet dann die Bildfigur.
Fertige mehrere solcher Bildfiguren an, indem du den Stift ausschaltest, den Vergrößerungsfaktor und/oder den Punkt Z veränderst, den Stift wieder einschaltest und den Vorgang wiederholst.
Beobachte, welche Eigenschaften in allen Bildfiguren gleich sind.
Im folgenden Applet kannst du nun auch die Form und Lage des Dreiecks verändern, indem du seine Ecken an eine andere Stelle ziehst. Beobachte die Auswirkungen und formuliere weitere Eigenschaften der zentrischen Streckung.