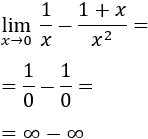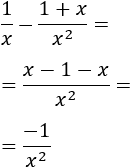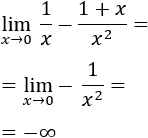Infinito menos infinito
En esta página proporcionamos algunos ejemplos de límites con la forma indeterminada infinito menos infinito y algunos métodos que podemos utilizar para evitarla. Especialmente, hablamos sobre los límites de polinomios y de restas de raíces.
1. Indeterminación ∞-∞
La expresión ∞-∞ es una indeterminación puesto aparece en el límite de algunas funciones cuyo límite es distinto. Por ejemplo,
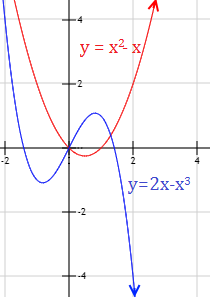
 Las gráficas de estas funciones son
Las gráficas de estas funciones son
 Por tanto, los límites anteriores son
Por tanto, los límites anteriores son
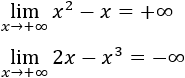 Es decir, tenemos la misma expresión algebraica (resta de infinitos), pero con resultados distintos.
Es decir, tenemos la misma expresión algebraica (resta de infinitos), pero con resultados distintos.
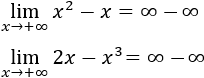 Las gráficas de estas funciones son
Las gráficas de estas funciones son
 Por tanto, los límites anteriores son
Por tanto, los límites anteriores son
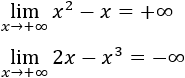 Es decir, tenemos la misma expresión algebraica (resta de infinitos), pero con resultados distintos.
Es decir, tenemos la misma expresión algebraica (resta de infinitos), pero con resultados distintos.2. Límite de un polinomio
Como las potencias de infinitos son infinitos, la resta de infinitos suele aparecer en el límite de los polinomios (cuando x tiende a infinito).
Dado un polinomio, cuando x toma valores grandes, los monomios que toman valores mayores (sin considerar el signo) son los que tienen mayor grado.
Por ejemplo, consideremos la función f(x) = x2 – x. Damos valores a x:
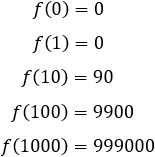 La función toma valores cada vez mayores porque el monomio de grado 2 crece más rápido que el de grado 1. Dicho en otras palabras, el infinito del monomio de grado 2 es de orden mayor que el del monomio de grado 1.
Podemos deducir que el límite es infinito positivo:
La función toma valores cada vez mayores porque el monomio de grado 2 crece más rápido que el de grado 1. Dicho en otras palabras, el infinito del monomio de grado 2 es de orden mayor que el del monomio de grado 1.
Podemos deducir que el límite es infinito positivo:
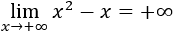 Por tanto, para calcular el límite, tenemos que fijarnos en el orden de los infinitos. En el límite de un polinomio, la resta de infinitos es el infinito de mayor orden (el infinito que corresponde al monomio de grado mayor es el de mayor orden).
Esto implica que, además, el signo del resultado depende del coeficiente del monomio de grado mayor. Por ejemplo,
Por tanto, para calcular el límite, tenemos que fijarnos en el orden de los infinitos. En el límite de un polinomio, la resta de infinitos es el infinito de mayor orden (el infinito que corresponde al monomio de grado mayor es el de mayor orden).
Esto implica que, además, el signo del resultado depende del coeficiente del monomio de grado mayor. Por ejemplo,
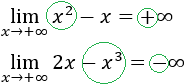 Cuando x tiende a infinito negativo, es un poco más complicado. En este caso, lo más sencillo es sustituir, calcular los signos (depende de la paridad de las potencias) y comparar el orden de cada infinito.
Por ejemplo,
Cuando x tiende a infinito negativo, es un poco más complicado. En este caso, lo más sencillo es sustituir, calcular los signos (depende de la paridad de las potencias) y comparar el orden de cada infinito.
Por ejemplo,
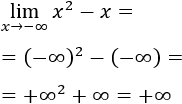 El resultado es infinito positivo porque el signo del infinito de mayor orden es positivo.
El resultado es infinito positivo porque el signo del infinito de mayor orden es positivo.
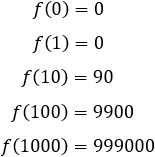 La función toma valores cada vez mayores porque el monomio de grado 2 crece más rápido que el de grado 1. Dicho en otras palabras, el infinito del monomio de grado 2 es de orden mayor que el del monomio de grado 1.
Podemos deducir que el límite es infinito positivo:
La función toma valores cada vez mayores porque el monomio de grado 2 crece más rápido que el de grado 1. Dicho en otras palabras, el infinito del monomio de grado 2 es de orden mayor que el del monomio de grado 1.
Podemos deducir que el límite es infinito positivo:
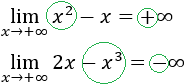 Cuando x tiende a infinito negativo, es un poco más complicado. En este caso, lo más sencillo es sustituir, calcular los signos (depende de la paridad de las potencias) y comparar el orden de cada infinito.
Por ejemplo,
Cuando x tiende a infinito negativo, es un poco más complicado. En este caso, lo más sencillo es sustituir, calcular los signos (depende de la paridad de las potencias) y comparar el orden de cada infinito.
Por ejemplo,
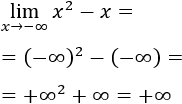 El resultado es infinito positivo porque el signo del infinito de mayor orden es positivo.
El resultado es infinito positivo porque el signo del infinito de mayor orden es positivo.3. Límite de una resta de raíces
Otro ejemplo típico de la indeterminación ∞-∞ es el de la resta de raíces. Por ejemplo,
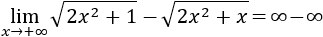 En estos límites, suele ser suficiente operar para transformar la resta de raíces en una suma. En el caso de las raíces cuadradas, multiplicamos y dividimos por la suma de raíces.
Por ejemplo,
En estos límites, suele ser suficiente operar para transformar la resta de raíces en una suma. En el caso de las raíces cuadradas, multiplicamos y dividimos por la suma de raíces.
Por ejemplo,
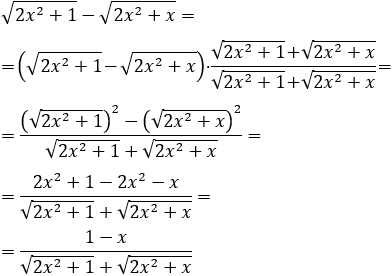 De este modo, la indeterminación desaparece:
De este modo, la indeterminación desaparece:
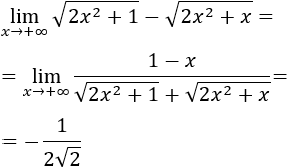 El resultado del límite es el coeficiente principal puesto que el grado de numerador y denominador son iguales.
Si las raíces son de otro orden, tenemos que utilizar las fórmulas que les corresponden. Por ejemplo, para raíces cúbicas,
El resultado del límite es el coeficiente principal puesto que el grado de numerador y denominador son iguales.
Si las raíces son de otro orden, tenemos que utilizar las fórmulas que les corresponden. Por ejemplo, para raíces cúbicas,
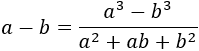
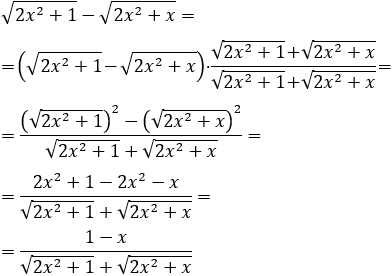 De este modo, la indeterminación desaparece:
De este modo, la indeterminación desaparece:
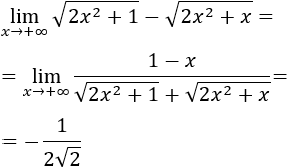 El resultado del límite es el coeficiente principal puesto que el grado de numerador y denominador son iguales.
Si las raíces son de otro orden, tenemos que utilizar las fórmulas que les corresponden. Por ejemplo, para raíces cúbicas,
El resultado del límite es el coeficiente principal puesto que el grado de numerador y denominador son iguales.
Si las raíces son de otro orden, tenemos que utilizar las fórmulas que les corresponden. Por ejemplo, para raíces cúbicas,
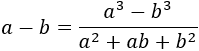
Más ejemplos en indeterminación infinito menos infinito.