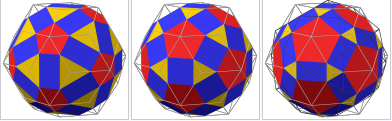
Images . Rhombicosidodecahedron (V=60) from Biscribed Pentakis Dodecahedron for the case of trisection of its 8th-order segments(Variant1)
Generating Elements of mesh modeling the surfaces of polyhedron, its dual image and the coloring of their edges and faces can be found in the applet.
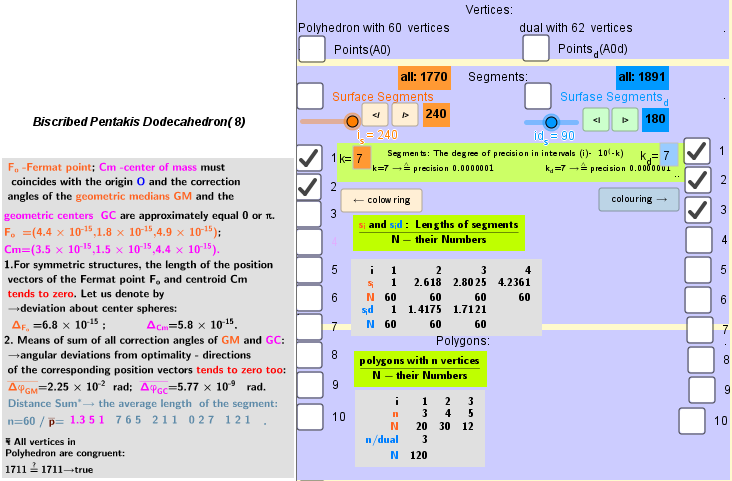
Elements in polyhedron Biscribed Pentakis Dodecahedron(8) :
Vertices: V=60.
Faces: F=62. (20 equilateral triangles{3} + 30 rectangles{4} + 12 regular pentagons{5})
Edges: E=120. 60+60 - The order of the number of edges in this polyhedron are according to their length.
Rhombicosidodecahedron:
Type Archimedean solid; Uniform polyhedron
Elements F = 62, E = 120, V = 60 (χ = 2)
Faces by sides 20{3}+30{4}+12{5}

Faces and Edges of the Biscribed Pentakis Dodecahedron(8) -Rhombicosidodecahedron (n=60)
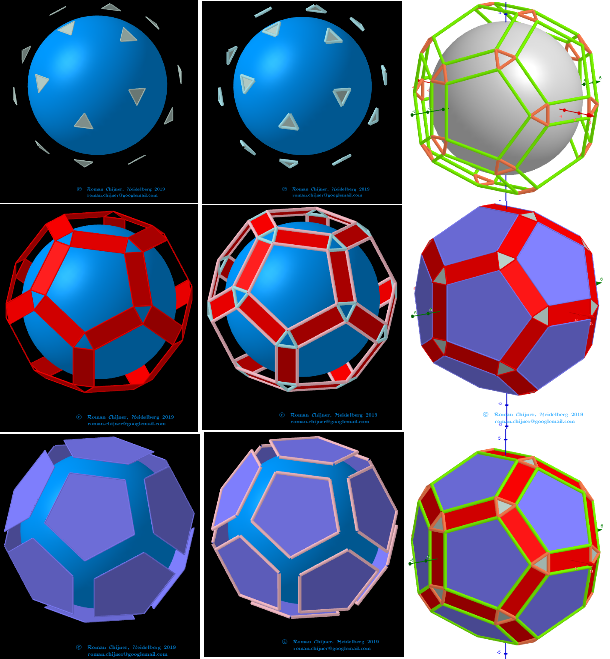
The elements of the dual to the Biscribed Pentakis Dodecahedron(8):
Vertices: V=62
Faces: F=120. 120 scalene triangles {3}
Edges: E=180. 60+60+60 - The order of the number of edges in this polyhedron are according to their length.
If we assume that two triangles with a common long side lie in the same plane, we get:
Vertices: V=62
Faces: F=60. 60 kites{4}
Edges: E=120. 60+60
Deltoidal Hexecontahedron :
Vertices: 62 = 12 + 20 + 30
Face polygon: 60 kites{4}
Edges: 120