Las coordenadas y los números positivos y negativos (I)
Prepara el entorno de trabajo
Comprueba que se visualizan la vista algebraica y la vista gráfica. Comprueba que se ven los ejes y la cuadrícula. Desplaza la zona gráfica para que los ejes queden centrados.
Dibuja un punto A cualquiera. Por ejemplo A(4,2). Desplaza el punto por la zona gráfica y observa en la vista algebraica como sus coordenadas cambian. Las coordenadas nos permiten conocer la ubicación del punto.
El punto B
En la línea de entrada escribe:
B=(2,y(A)). Mueve el punto A y observa como el punto B también se mueve. Observa las coordenadas del punto A y las coordenadas del punto B en la ventana algebraica.
1.- Mueve el punto A y escribe cinco ejemplos de coordenadas enteras del punto A y las correspondientes coordenadas enteras del punto B.
- Cuando el punto A tiene coordenadas (....,.....) el punto B tiene coordenadas (....,....)
- Cuando el punto A tiene coordenadas (....,.....) el punto B tiene coordenadas (....,....)
- Cuando el punto A tiene coordenadas (....,.....) el punto B tiene coordenadas (....,....)
- Cuando el punto A tiene coordenadas (....,.....) el punto B tiene coordenadas (....,....)
- Cuando el punto A tiene coordenadas (....,.....) el punto B tiene coordenadas (....,....)
Ten presente que B lo hemos definido de la siguiente manera B=(2,y(A)). Vas a descubrir que es esto de "y(A)".
2.- Completa: Cuando muevo el punto A, la primera coordenada de B siempre es ..... y la segunda coordenada de B siempre es igual a la ................ Por tanto deduzco que y(A) es la ............ y que x(A) querrá decir la .................. .
En la línea de entrada escribe B=(-x(A),y(A))El punto C
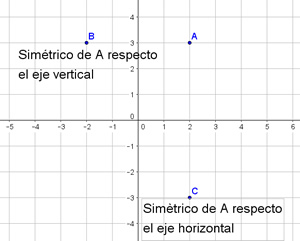
Dibuja un punto C que sea el simétrico del punto A respecto el eje horizontal (también llamado eje de abscisas o eje OX). Mueve el punto A y comprueba si el punto C es siempre el simétrico respecto el eje horizontal.
6.- ¿Qué has escrito en la línea de entrada para definir el punto C?
El punto D
Dibuja un punto D que sea el simétrico del punto A respecto el origen de coordenadas, es decir, que el origen de coordenadas sea el punto medio de A y D. Mueve el punto A y comprueba que el punto D también se mueve y siempre és el simétrico respecto el origen de coordenadas.
7.- ¿Qué has escrito en la línea de entrada para definir el punto D?
La simetria, las coordenadas y el opuesto
8.- Haz una síntesis de la relación entre simetria, coordenadas de un punto y opuesto de un número.