I. 5. Matrix representation of reflection
Estimate parameter a so that the matrix M represents reflection in line.
1. method: Rotation is a direct isometry, hence |A| = 1, i.e. .
2. method (experimental): Use tool slider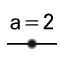
for unknown parameter a. Define one parameter family of matrices M(a).
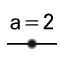for unknown parameter a. Define one parameter family of matrices M(a).
M ={{-0.5,a},{a,0.5}}
Draw arbitrary object B (point, segment or picture) and its image B' - GeoGebra command ApplyMatrix(matrix,object). Observe the effect of changing the slider a and estimate correct value for parameter a.
Experimental method is efficient for determination of fixed point and directions. Compare the position of arbitrary movable point B and its image B'. Find out the location where points coincide, B = B'. There is the fixed point of transformation. The same method applyed on line f gives you fixed direction. You should find the position where f is parallel with image f'.