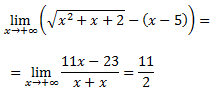Indeterminación infinito dividido (menos) infinito
Introducción
En ocasiones, al calcular límites encontramos ciertas expresiones cuyos valores no conocemos a priori. Son las llamadas indeterminaciones. Para algunas de ellas existen reglas que nos permiten calcular su valor (como en el caso de 1 ∞ ). Pero la mayoría de las indeterminaciones no se resuelven de un modo tan directo, sino que debemos realizar una serie de operaciones o cálculos para poder determinar sus valores. Debemos decir que en realidad, el cálculo diferencial nos proporciona un método muy efectivo y sencillo bajo ciertas condiciones: la Regla de L'Hôpital. Vamos a ver cómo podemos resolver las indeterminaciones y .
1. Cociente de infinitos
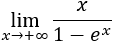
Tenemos una indeterminación:
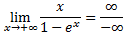
Sin embargo, sabemos que la exponencial crece mucho más rápido que un polinomio de grado 1, por tanto, es como si en el denominador tuviéramos un polinomio de grado mucho mayor. De este modo,
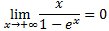
Ejemplo 2
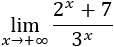
Tenemos de nuevo la indeterminación . Para evitarla, dividimos el numerador y el denominador por la exponencial de base mayor:
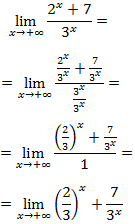
Sabemos que
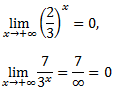
Por tanto,
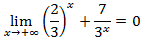
2. Diferencia de infinitos del mismo orden
Suele ocurrir cuando tenemos una resta de raíces o de exponenciales. En el primer caso, se multiplica y divide por el conjugado (si las raíces son cuadradas). En el segundo, multiplicamos y dividimos por la exponencial de base mayor.
Ejemplo 3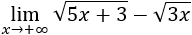
Primero, lo que hacemos es quedarnos con los monomios que tienen mayor grado.
Después escribimos la función como un producto y el límite es directo:
Notemos que el signo del infinito es positivo ya que .
Ejemplo 4
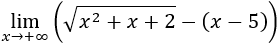
Como tenemos una resta de infinitos, vamos a multiplicar y a dividir por el conjugado (real). Recordemos que el conjugado de a+b es a-b.
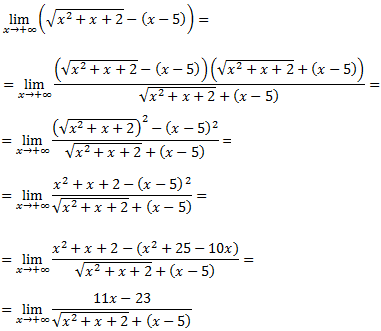
Notemos que hemos conseguido un polinomio (de grado 1) en el numerador y el denominador no es un problema ya que se trata de una suma (lo sería en caso de ser una resta). Nos quedamos con el monomio de grado mayor del radicando para obtener un cociente de polinomios.
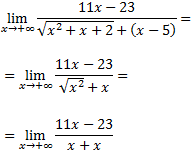
Luego tenemos un cociente de polinomios del mismo grado y el límite es al infinito, por tanto,
