Operaciones entre Sucesiones
Suma (o resta)
Sean a(n) y b(n) dos sucesiones, entonces su suma es la sucesión c(n) definida por
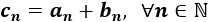Convergencia de la suma: Si las sucesiones a(n) y b(n) son convergentes a A y a B, respectivamente, entonces c(n)=a(n)+b(n) es convergente a A+B:
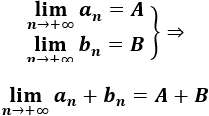Si una o las dos sucesiones a(n) y b(n) son divergentes, la suma puede ser convergente o divergente.
Ejemplo: La resta de las sucesiones a(n)=n y b(n)=2n es
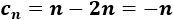Primeros términos:
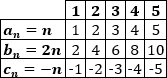Las dos sucesiones son divergentes y su resta c(n) también es divergente:
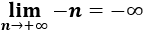
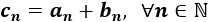Convergencia de la suma: Si las sucesiones a(n) y b(n) son convergentes a A y a B, respectivamente, entonces c(n)=a(n)+b(n) es convergente a A+B:
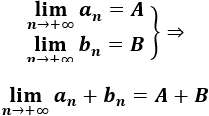Si una o las dos sucesiones a(n) y b(n) son divergentes, la suma puede ser convergente o divergente.
Ejemplo: La resta de las sucesiones a(n)=n y b(n)=2n es
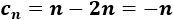Primeros términos:
Las dos sucesiones son divergentes y su resta c(n) también es divergente:
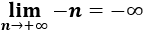
Producto
Sean a(n) y b(n) dos sucesiones, entonces su producto es la sucesión c(n) definida por
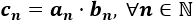Convergencia del producto: Si las sucesiones a(n) y b(n) son convergentes a A y a B, respectivamente, entonces c(n)=a(n)⋅b(n) es convergente a A⋅B:
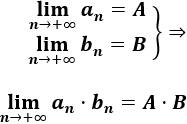
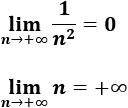El producto de las sucesiones es
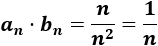Es una sucesión convergente:
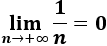
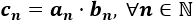Convergencia del producto: Si las sucesiones a(n) y b(n) son convergentes a A y a B, respectivamente, entonces c(n)=a(n)⋅b(n) es convergente a A⋅B:
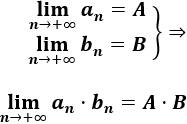
- Si a(n) converge a L≠0 y b(n) diverge, su producto es divergente.
- Si a(n) converge a L=0 y b(n) diverge, su producto puede ser convergente o divergente.
- Si las sucesiones a(n) y b(n) son divergentes, su producto es divergente.
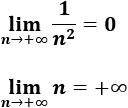El producto de las sucesiones es
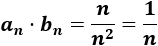Es una sucesión convergente:
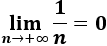
Cociente
Sean a(n) y b(n) dos sucesiones, siendo b(n)≠0, entonces su cociente es la sucesión c(n) definida por
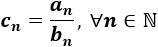Convergencia del cociente: Si las sucesiones a(n) y b(n) son convergentes a A y a B≠0, respectivamente, entonces c(n)=a(n)/b(n) es convergente a A/B:
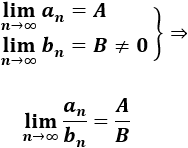
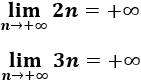El cociente de las sucesiones es una sucesión constante y, por tanto, convergente:
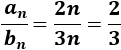
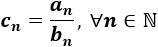Convergencia del cociente: Si las sucesiones a(n) y b(n) son convergentes a A y a B≠0, respectivamente, entonces c(n)=a(n)/b(n) es convergente a A/B:
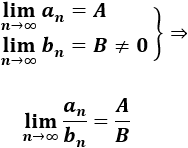
- Si a(n) converge y b(n) diverge, su cociente es convergente a 0.
- Si a(n) converge y b(n) converge a L=0, su cociente diverge.
- Si a(n) diverge y b(n) converge a L≠0, su cociente diverge.
- Si a(n) diverge y b(n) converge a 0, su cociente puede ser convergente o divergente.
- Si las sucesiones a(n) y b(n) son divergentes, su cociente puede ser convergente o divergente.
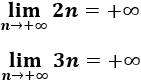El cociente de las sucesiones es una sucesión constante y, por tanto, convergente:
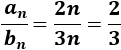
Más información: Operaciones entre sucesiones (definición, convergencia y problemas resueltos)
Otros recursos de sucesiones:
- Test básico
- Tipos de sucesiones
- Progresiones aritméticas
- Progresiones geométricas
- Problemas de progresiones aritméticas y geométricas
- Sucesión de Fibonacci
- Calculadoras de progresiones aritméticas
- Calculadoras de progresiones geométricas
- Operaciones entre sucesiones
- Límites de sucesiones
- Subsucesiones
- Introducción a las sucesiones (PyE)
- Criterio de la media aritmética
- Criterios de la media geométrica y de la raíz
- Criterio de Stolz del cociente