7.4 Evaluate Logarithms and Graph Logarithmic Functions
Intro to Logarithms
Logarithms can be thought of as taking the inverse of the exponent function.
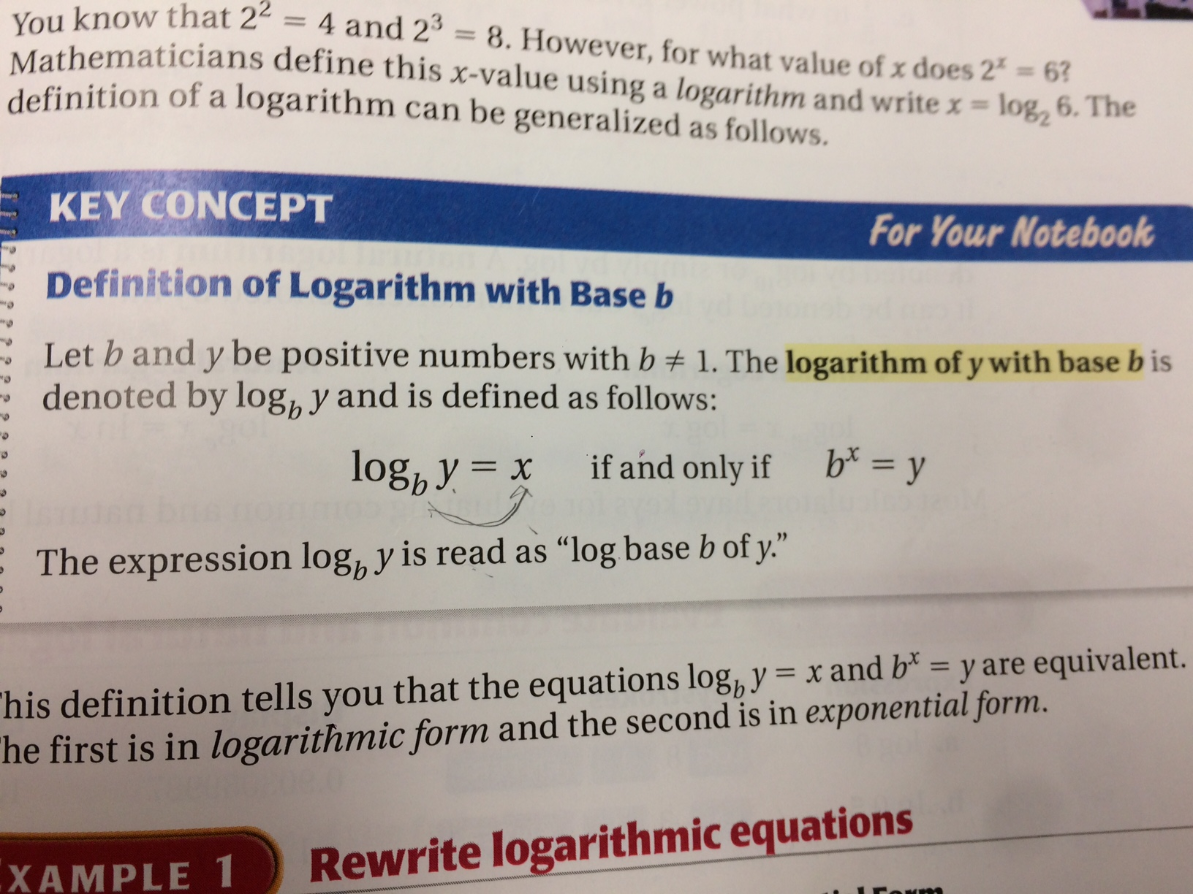
Practice Makes Perfect
Before we begin exploring, we will practice the purely algebraic techniques involving Logarithms.
(Littell)
Ex. 1
Ex. 2
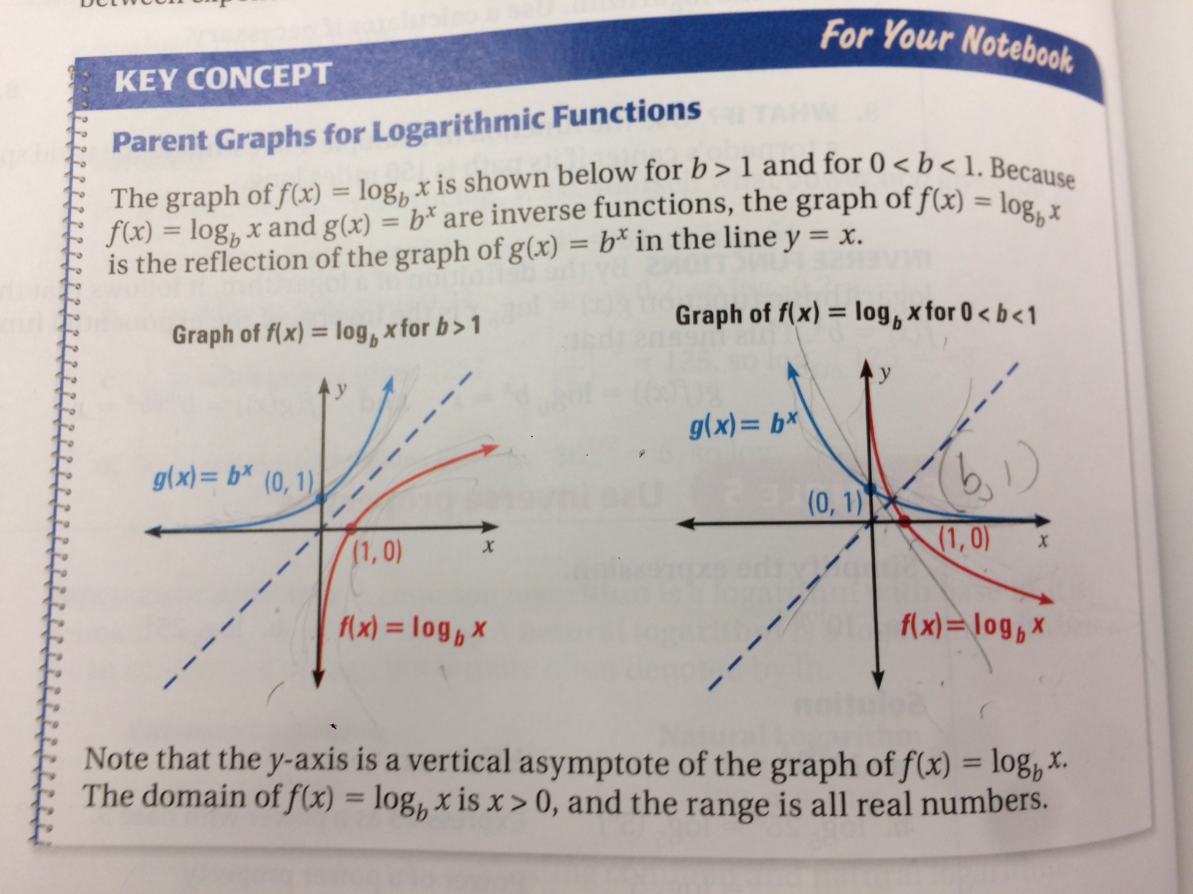
Graphing the Logarithmic Function
Concept: Because the logarithmic function and exponential function are inverse of each other, the graph of the logarithmic function will be a reflection of the exponential function on the other side of the y = x line.
Model Reference
Tim Brzezinski
https://www.geogebra.org/tbrzezinski
Instructions for Model
1) Play with the a slider. This is the base of the logarithm. Recall what role this plays in the exponential function.
2) Next, play with the c slider. What are the similarities and differences with this and exponential growth and decay.
3) Play with the k slider. What does this do to the graph?
4) Play with d. What does this do to the graph?