x² + x₁
Esta actividad pertenece al libro de GeoGebra Julia y Mandelbrot.
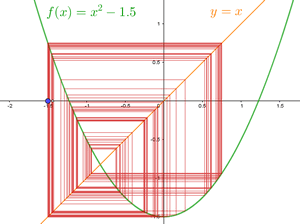
Imagina que partes de un número cualquiera x1, por ejemplo, el 2. Lo elevas al cuadrado y le sumas el número de partida (22 + 2). El resultado es 6. Elevas este resultado al cuadrado y le sumas el número de partida. Obtienes 38. Luego elevas este número al cuadrado y vuelves a sumarle 2, y así sucesivamente, en cada paso elevas al cuadrado el resultado obtenido en el paso anterior y le sumas el número de partida.
Obtendrás la sucesión: {2, 6, 38, 1446, 2090918, ...}. Está claro que esta sucesión no parará de crecer en cada paso, y además, crecerá cada vez a mayor ritmo, superando cualquier límite que fijemos de antemano, por grande que sea. Es decir, no está acotada.
- Nota: Estas sucesiones son muy fáciles de obtener usando la hoja de cálculo. En la celda A1 pones el 2. En la casilla A2 escribes la fórmula A$1 + A1^2. Ahora solo tienes que arrastrar esta celda hacia abajo para obtener los siguientes valores. Observa que todos los valores dependen únicamente del valor del primer elemento, A1.
- Por ejemplo, mientras que toda la sucesión que empieza en 0.25 se mantiene por debajo de 0.5, la que parte de 0.250001 supera el valor 0.5 en el paso 1562, supera el 1 en el paso 3163 y vale más de 40.000 solo seis pasos después.
{-1.5, 0.75, -0.9375, -0.62109, -1.11424, -0.25846, -1.4332, 0.55405, ...}
Podemos apreciar mejor este comportamiento caótico usando gráficas. En la siguiente imagen, hemos colocado los 100 primeros valores de esa sucesión en el eje Y, mientras que en el eje X colocamos el número de paso (1, 2, 3, 4 ...), como si fuese el transcurrir del tiempo: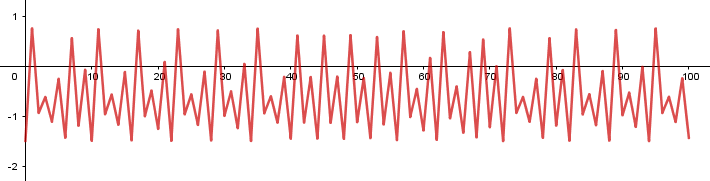
- Si partimos de -2, la sucesión se vuelve constante en 2.
- Si partimos de un valor entre -2 y -1, la sucesión es caótica.
- Si partimos de -1, la sucesión es alternada.
- Si partimos de un valor entre -1 y 0, la sucesión es convergente.
- Si partimos de 0, la sucesión es constante.
- Si partimos de un valor entre 0 y 0.25, la sucesión es convergente.
Autor de la actividad y construcción GeoGebra: Rafael Losada.