Cone of Maximum Volume (Calculus: Optimization)
Classic Calculus Conundrum
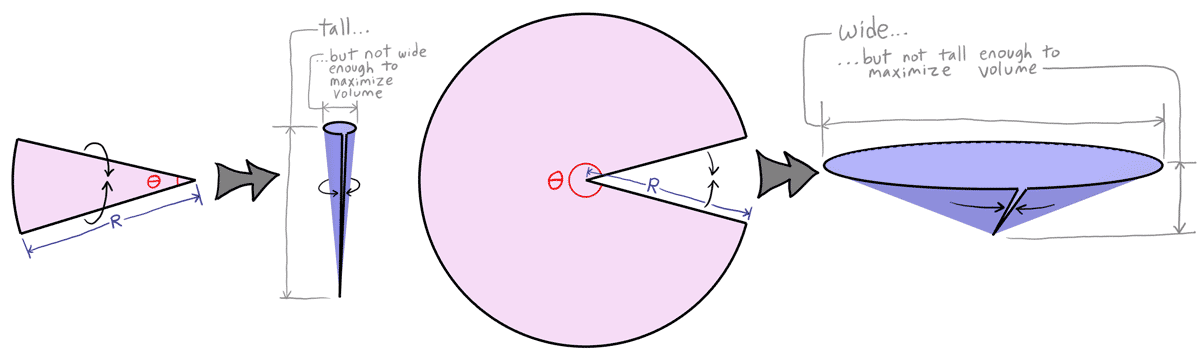
Consider a sector (i.e. slice of pizza) with central angle θ and radius R. The straight edges of the sector are brought together to form a cone.
If θ is too small, the resulting cone is relatively “tall but skinny,” and therefore has a relatively small volume.
If θ is too large, the resulting cone is relatively “wide but short,” and therefore has a relatively small volume.
Challenge: Find the optimal angle θ such that the volume of the cone is maximized.
The best way to visualize the puzzle is to cut sectors from paper and roll them into cones and speculate when volume is maximized. This GeoGebra construction merely offers an alternative means to visualize and explore the premise. The calculus-derived solution to this puzzle is not presented here.
The various controls on the left side of the GeoGebra view below should become self-evident with a little exploration. Click/drag or use typical touchscreen gestures to alter the perspective in the 3D graphics view on the right.
Finer control of sliders via keyboard may be achieved by selecting slider dot and then using arrow keys to adjust values. Change increments by holding down either Shift or Ctrl key while using arrow keys.