원뿔의 절단과 원뿔곡선
본 학습 자료는 『Modern Geometry with Applications』 (George A. Jennigs)의 내용을 바탕으로 만들었습니다.
3차원 공간에 한 점 에서 만나는 두 직선 , 에 대하여 직선 이 직선 을 중심으로 회전하여 얻은 곡면을 직원뿔(이하 원뿔)이라고 한다. 직선 을 직선 을 중심으로 회전하여 얻어지는 모든 직선을 원뿔의 모선, 직선 은 원뿔의 축이라 한다. 점 는 원뿔의 꼭짓점이라 하며, 일반적인 용어는 아니지만 직선 과 이 이루는 예각 를 원뿔의 꼭짓점 반각이라고 하자.
아래 지오지브라 애플릿을 통해 직원뿔을 관찰해보세요.
한 평면이 만나서 원뿔과 만나서 생기는 교선(또는 교점)을 원뿔곡선(conic section)이라고 한다. 본 자료의 나머지 부분에서는 다음과 같은 표기법을 사용하고자 한다.
- : 꼭짓점이 인 원뿔
- : 원뿔과 만나는 평면
- : 원뿔 와 평면 의 교선
- : 원뿔 의 꼭짓점 반각
- : 원뿔 의 축과 평면 가 이루는 각
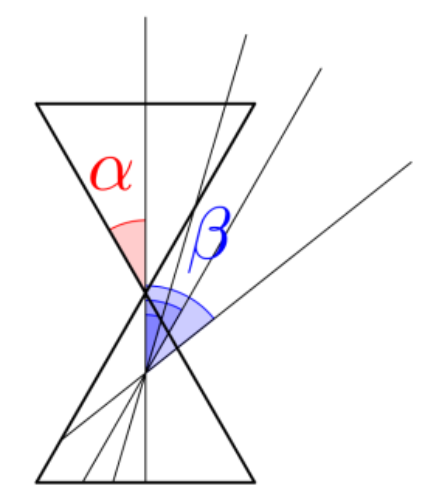
원뿔곡선의 모양은 다음과 같은 두 가지 사항에 의해 결정된다.
① 평면 가 꼭짓점 를 포함하느냐에 따라,
a. 포함하면, 퇴화(degenerate)
b. 포함하지 않으면, 매끄러운(smooth)
② 두 각 , 의 크기에 따라
ⅰ. 이면, 타원
ⅱ. 이면, 포물선
ⅲ. 이면, 쌍곡선
이라고 한다. 따라서 원뿔곡선은 아래 그림과 같이 여섯 가지 모양의 원뿔곡선이 나타난다. 퇴화 쌍곡선은 점 에서 만나는 두 직선이며, 퇴화 포물선은 한 직선, 퇴화 타원은 한 점이다.
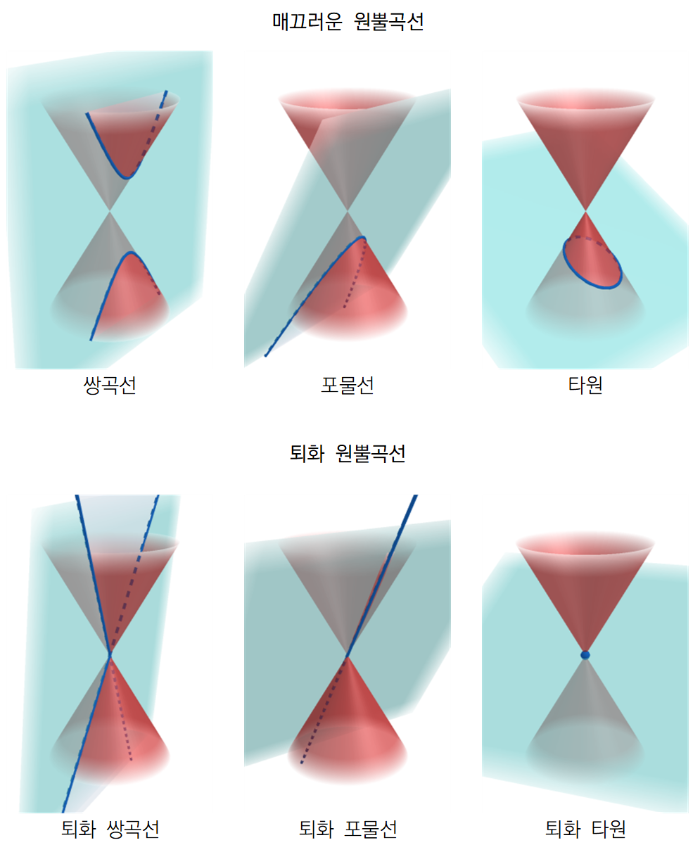
아래 지오지브라 애플릿에서 두 각 , 의 크기를 조절하며 퇴화 및 매끄러운 원뿔곡선을 관찰해보세요.
여섯 가지 원뿔곡선
탐구문제(해시계)
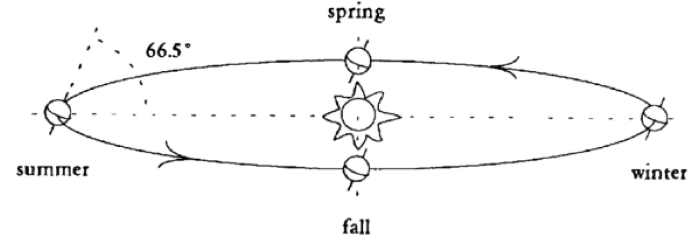
일반적인 해시계는 수평면과 수직 포인터 또는 노먼으로 구성된다. 태양이 하늘을 가로질러 이동할 때, 노먼의 그림자는 평면을 가로질러 이동한다. 그림자의 위치는 하루의 시계를 알려준다.
움직이는 그림자의 끝이 그리는 자취 곡선은 두 가지 요소에 따라 달라진다.
- 해시계가 있는 곳의 위토(노먼과 지구의 자전축 사이의 각의 크기 결정)
- 계절(지구 공전궤도에서 지구의 위치를 결정하므로 태양빛이 지표면과 이루는 각의 크기를 결정)