Looking Through Spectacles
Can you see clearly through those spectacles?

OBJECTIVE: To learn how to find the least common multiple (LCM)
In previous lessons, you've learned about prime factorization, prime and composite numbers, factors and multiples, and divisibility rules. You also learned how to find the GREATEST COMMON FACTOR (GCF).
Climbing Down Trees: https://www.geogebra.org/m/hxmuf2dg
Going Dutch: https://www.geogebra.org/m/xvdee7pg
Sifting Grains: https://www.geogebra.org/m/gamspcmt
Looking through the Lens: https://www.geogebra.org/m/arz3t78a
In this lesson, you'll learn how to find the LEAST COMMON MULTIPLE (LCM), also known as LEAST COMMON DENOMINATOR (LCD).
The LEAST COMMON MULTIPLE (LCM) of two or more counting numbers is the smallest counting number that is divisible by all the given numbers. Just as in the case of the GCF, there are many approaches to finding LEAST COMMON MULTIPLE (LCM). So let's just follow a parallel process similar to finding the GREATEST COMMON FACTOR (GCF)—Factor Tree, Venn Diagram, and Continuous Division.
FACTOR TREE
If we use the FACTOR TREE, we have to list down the prime factors of the numbers whose LCM we're trying to find. Then we multiply the common prime factors just as in finding the GCF, but in addition, we multiply the factors that have been left out to the result. The final result we get is the LCM.
Example: What is the LCM of 16 and 24?
Prime factors of 16 : 2 x 2 x 2 x 2
Prime factors of 24 : 2 x 2 x 2 x 3
The product of the common factors, 2 x 2 x 2 = 8, which is the GCF.
The product of the GCF and what have been left out, 8 x 2 x 3 = 48, which is the LCM.
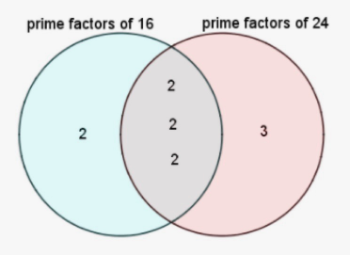
VENN DIAGRAM
If we use the Venn Diagram, we can list the common prime factors of 16 and 24 inside the lens (the intersection of the two sets), while the other prime factors are listed inside their respective crescents. We then multiply the numbers inside the lens together with the numbers in the remainder of the spectacles, as follows: 2 x 2 x 2 x 2 x 3 = 48. The LCM is 48.
CONTINUOUS DIVISION
If we use CONTINUOUS DIVISION, we follow the same procedure as for finding the GCF, but we use a different formula for multiplying the factors. Instead of just using the numbers on the left, we include the numbers at the bottom in the multiplication to find the LCM.
 The LCM is 2 x 2 x 2 x 2 x 3 = 48.
Here's an example using three numbers.
The LCM is 2 x 2 x 2 x 2 x 3 = 48.
Here's an example using three numbers.
 The LCM is 2 x 2 x 3 x 3 x 2 x 3 x 5 = 1,080.
CAVEAT: For three or more numbers, division by prime factors must be continued until all the numbers in the bottom row are RELATIVELY PRIME, meaning no two numbers must share a common factor. The example below illustrates this important rule.
The LCM is 2 x 2 x 3 x 3 x 2 x 3 x 5 = 1,080.
CAVEAT: For three or more numbers, division by prime factors must be continued until all the numbers in the bottom row are RELATIVELY PRIME, meaning no two numbers must share a common factor. The example below illustrates this important rule.
 The LCM is 10 x 2 x 3 x 7 x 2 x 2 x 5 = 8,400.
Notice that in the second to the last row, only 2 and 4 have a common factor, but we still had to factor out that common factor. If we didn't do that, the LCM would appear to be 16,800, which is WRONG!
The LCM is 10 x 2 x 3 x 7 x 2 x 2 x 5 = 8,400.
Notice that in the second to the last row, only 2 and 4 have a common factor, but we still had to factor out that common factor. If we didn't do that, the LCM would appear to be 16,800, which is WRONG!
Use the applet below for practice.
Enter 2 numbers in the entry boxes. Try solving the problem first on a separate sheet of paper, and then verify your answer by clicking Show Solutions. The applet will generate consecutive multiples of the two numbers, which may or may not contain the LCM, depending on the size of the numbers you enter. In any case, the LCM will appear between the two columns.
Click LCM for 3 Numbers to work on 3 numbers, and follow the same procedure.
Repeat as many times as needed to master the concept.
In this lesson, you learned how to find the Least Common Multiple.
Future lessons will include the applications of the GCF and LCM. Did you ENJOY today's lesson?