Visualisierung von Brüchen mithilfe von Lissajous-Figuren
Mathematik kann schön sein und Zahlen haben ihre Visualisierung.
Lissajous-Figuren sind Beispiele für solche Visualisierungen. Sie entstehen beim Zusammenspiel von Schwingungen. Häufig erscheinen diese Figuren in Science-Fiction-Filmen auf irgendwelchen Bildschirmen.
Du kannst in dem Applet die Punkte C und D auf den jeweiligen Kreisen in ihrer Ausgangslage durch Greifen verändern.
Man findet auf der Wikipedia-Seite verschiedene Lissajous-Figuren dargestellt.
Versuche fünf Figuren mit dem Applet zu erzeugen und beschreibe, was du hierzu gemacht hast bzw. was die Spalten- und Zeilenüberschriften bedeuten können.
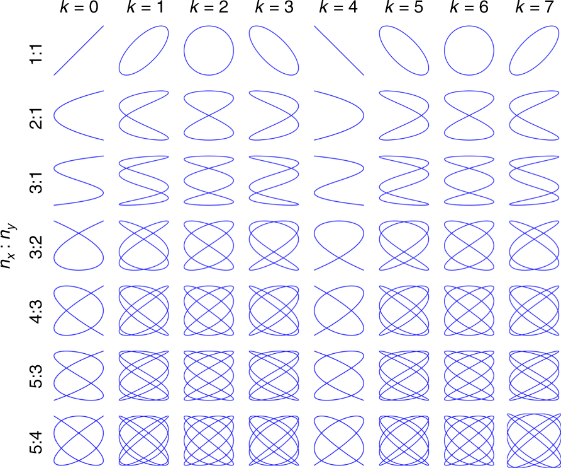
Ergänze: "Das Geschwindigkeitsverhältnis 4:3 bedeutet, wenn der Punkt C vier Umdrehungen macht, dann ..." "Der Punkt C ist ... so schnell wie ..."
Was haben Lissajous-Figuren mit Brüchen zu tun?
Untersuche den Zusammenhang der Lissajous-Figuren bei einem Bruch und dem entsprechenden Kehrbruch.
Untersuche, ob die Lissajous-Figur abhängig von der Startposition der Punkte C und D ist. Begründe.
Untersuche, für welche Verhältnisse die Lissajous-Figuren gleich sind. Gib mindestens drei verschiedene Verhältnisse an.
Forschungsfragen für Interessierte:
- Manchmal entstehen geschlossene Lissajous-Figuren, manchmal nicht. Gibt es da eine Regel?
- Gibt es einen Zusammenhang zwischen der Anzahl der Kreuzungen und dem "Geschwindigkeitsverhältnis"?