Claire Lommé - Démonstration du théorème de Pythagore
Etape 1 :
Sur l'appliquette ci-dessus, tracer le cercle de centre le point C passant par B.
Etape 2 :
Tracer la droite (AC), elle coupe le cercle en deux points R et U.
Tracer la droite (AB), elle recoupe le cercle au point S.
Tracer le triangle ASU.
Etape 3 :
Construire le triangle ARB.
On voit ainsi apparaître ces deux triangles T1 et T2 .
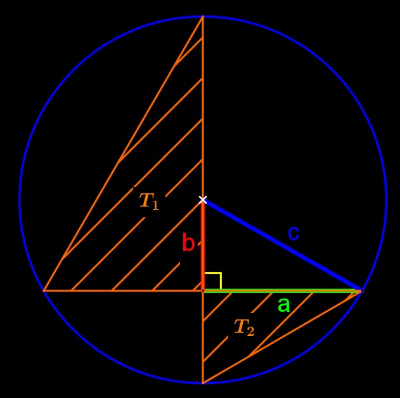
Dans l'appliquette ci-dessous, cliquer sur le bouton suivant pour mettre
en évidence deux angles.
Cliquer à nouveau sur le bouton suivant pour faire apparaître un arc de
cercle.
Ces deux angles ont quelque-chose de particulier, ils sont inscrits dans
un même cercle qu'ils coupent en un même arc de cercle, celui repassé
en jaune et qu'on vient de mettre en évidence.
On dit qu'ils interceptent le même arc de cercle.
Il existe un théorème, le théorème de l'angle inscrit, qui nous dit que,
comme ils interceptent le même arc de cercle, ces deux angles ont la
même mesure !
Vous trouverez une démonstration de ce théorème en cliquant sur ce lien
Revenons à nos deux triangle hachurés.
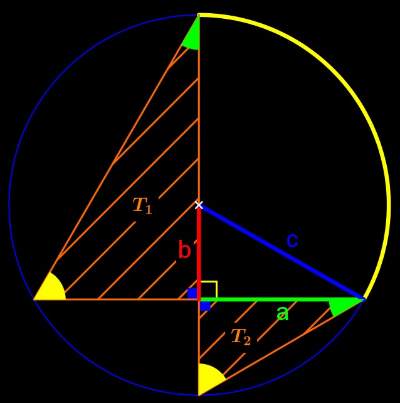
Les deux angles jaunes sont égaux,
chacun de ces deux triangles a aussi un angle droit,
Comme dans un triangle, en géométrie euclidienne, la somme des mesures des angles est égale à 180°, on en déduit que les deux angles codés ici en vert sont égaux aussi !
Autrement dit, les triangles T1 et T2 ont les mêmes mesures d'angles, ils sont donc semblables et leurs côtés sont deux à deux proportionnels !
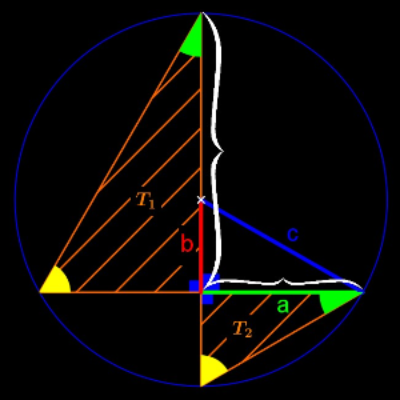
Les deux côtés marqués par une accolade sont ceux compris entre l'angle droit et l'angle vert, ils sont donc homologues. L'un d'eux mesure a. Exprimer l'autre en fonction de a, b et c :
Nous pouvons donc les placer dans une même colonne dans le tableau de proportionnalité obtenu :

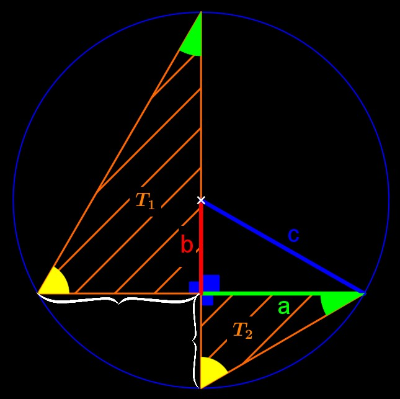
Ces deux autres côtés marqués par une accolade sont ceux compris entre l'angle droit et l'angle jaune, ils sont donc également homologues. L'un d'eux mesure a (puisqu'on se rend compte facilement que le diamètre porté par le côté rouge est la médiatrice de la corde portée par le segment vert). Exprimer l'autre en fonction de a, b et c :
Nous pouvons donc les compléter le tableau de proportionnalité :

Dans ce tableau de proportionnalité, les produits en croix sont égaux,

On en déduit donc l'égalité suivante :
(c + b)(c - b) = a²
Développer et réduire le membre de gauche de cette égalité :
Ajouter b² dans chaque membre de cette égalité :
Le théorème de Pythagore est ainsi démontré !