Intersección de dos cilindros (caso 1º)
Consideramos dos casos en cuanto a las posiciones relativas de los dos cilindros:
1. Ejes perpendiculares.
2. Ejes paralelos.
Caso 1.
Consideramos los cilindros de ecuaciones:
Cil1: y² + z² = s²
Cil2: x² + (z-c)² = r²
Donde r, s, son los radios respectivos, c la distancia entre los ejes. Sin pérdida de generalidad consideramos s ≥ r.
Haciendo z = c + r cos(t) se obtienen las ecuaciones paramétricas de la curva de intersección (caso que exista):
x = r sen(t)
y = sqrt(s² – (c + r cos(t))²)
z = c + r cos(t)
Según los valores de c en relación a s, r, se tienen las siguientes situaciones:
1.1. c = 0 (figura siguiente) Se obtienen dos curvas simétricas una respecto a la otra y cerradas. Las curvas son alabeadas y simétricas respecto a los planos OXY y OYZ.
1.2. 0 < c < s – r. El resultado es similar al anterior pero ahora las curvas son simétricas solo respecto a OYZ.
1.3. c = s – r. La intersección se reduce a una sola curva con un punto doble en (0,0,s).
La curva es parecida a una lemniscata, pero alabeada.
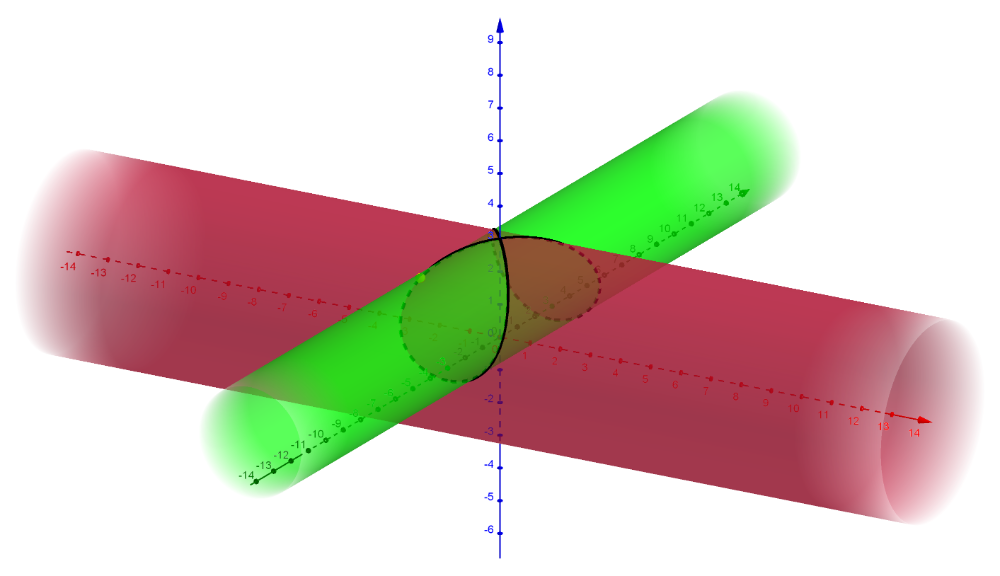
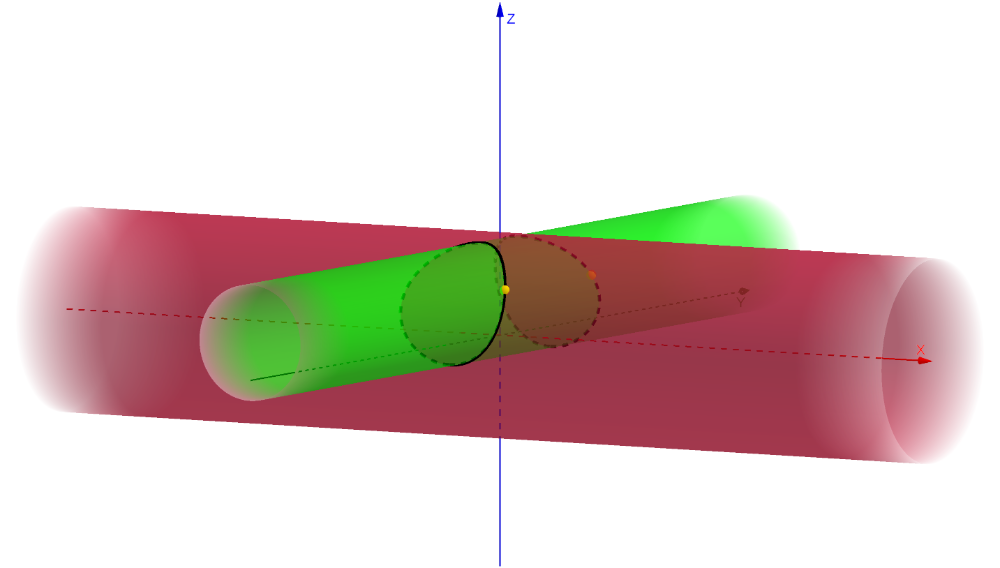
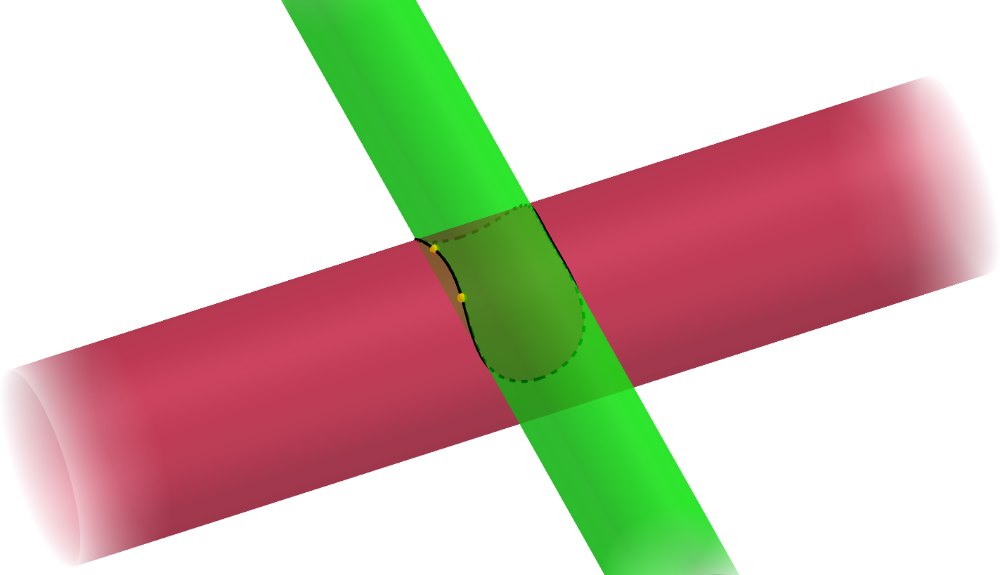
1.4. s – r < c < s + r. Se obtiene una curva alabeada sin puntos dobles, simétrica respecto a OYZ y OXZ.
Sus proyecciones sobre OXZ y OYZ son sendos arcos de circunferencia.
1.5. c > s + r. No hay intersección entre los dos cilindros.
