Überbestimmte LGS untersuchen
Übernahme aus der Mathelounge (Stefan aka Tschakabumba)
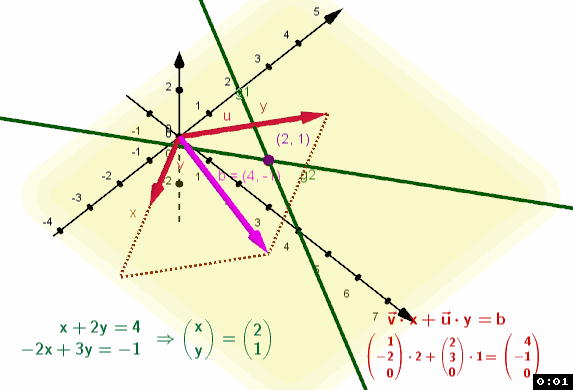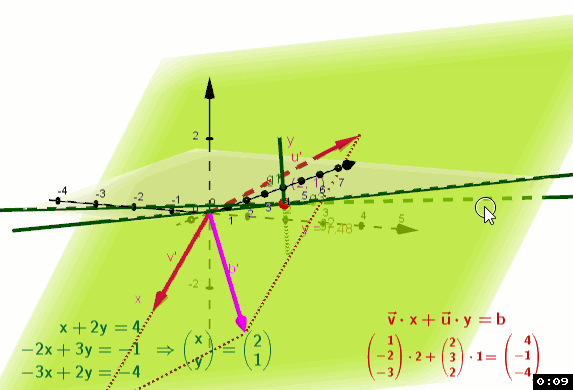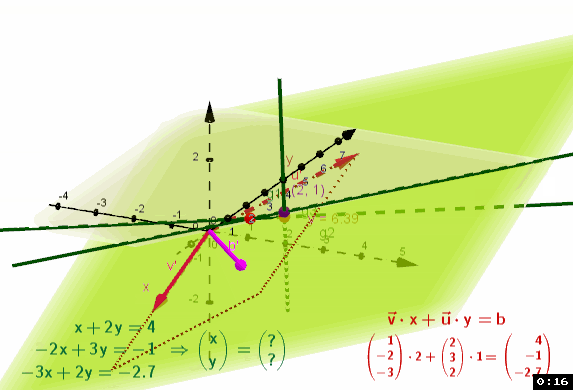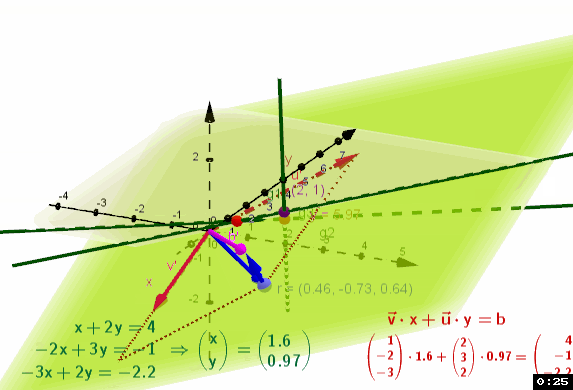
Wir betrachten folgende 3 Gleichungen mit 2 Variablen:
Du hast mehr Gleichungen als Variablen, solche Gleichungssysteme heißen "überbestimmt" und sind in der Regel nicht exakt lösbar. Du könntest x und y so bestimmen, dass 2 Gleichungen exakt gelöst werden, die dritte mit diesen x- und y-Werten aber völlig daneben liegt. Besser wäre es, eine Näherungslösung zu finden, die alle 3 Gleichungen "möglichst gut" erfüllt. Wenn z.B. x0=1.4 und y0=0.5 gewählt werden, erhalten wir folgende Abweichungen ri
Um diese Abweichungen ri zu minimieren, setzen wir das Problem nun auf eine geometrische Ebene.
Dazu schreiben wir die 3 Gleichungen auf in
Nicht lösbar ist das System deswegen, weil sich der Vektor b nicht als Linearkombination der Spaltenvektoren von A schreiben lässt. Mit dem Trick von oben addieren wir auf der rechten Seite einen "Rest-Vektor" r⃗ , den wir so wählen können, dass sich die komplette rechte Seite b⃗ +r⃗ als Linearkombination der Spaltenvektoren von A schreiben lässt:
Geometrisch bedeutet dies Folgendes. Der Vektor b⃗ liegt außerhalb der (Hyper-)Ebene, die durch die Spaltenvektoren von A aufgespannt wird. Durch Addition eines geeigneten Vektors r⃗ zu b⃗ können wir jedoch bewirken, dass der Summenvektor b⃗ +r⃗ in dieser (Hyper-)Ebene liegt. Für r⃗ muss dafür nur
r⃗ =A x⃗ −b⃗
gelten, ansonsten können wir ihn noch frei wählen. Die Idee hinter der Normalengleichung ist nun, diesen Vektor r⃗ "möglichst kurz" zu wählen. Der Vektor r⃗ ist genau dann am kürzesten, wenn er senkrecht auf der (Hyper-)Ebene steht, die durch die Spaltenvektoren von A aufgespannt wird. Aus Sicht des Endpunktes von b⃗ geht es dann nämlich direkt senkrecht in Richtung (Hyper-)Ebene. Wenn der Vektor r⃗ aber senkrecht auf dieser (Hyper-)Ebene steht, dann steht er auch senkrecht auf allen Spaltenvektoren von A, die diese (Hyper-)Ebene aufspannen. Das Skalarprodukt aus allen Spaltenvektoren von A und r⃗ muss also 0 sein. Bei der Matrix-Multiplikation heißt es "Zeile mal Spalte", daher können wir die Matrix A zu AT transponieren und die gefundene Bedinung in der Form AT⋅r⃗ =0⃗ formulieren. Das bedeutet:
| LGS | Matrix-Schreibweise und | Vektor-Schreibweise |
LGS_Interpretieren_Zeilen.SpaltenR2R3Normalengleichg
In der App verwende ich von der Einführung abweichende Gleichungen, die in der Darstellung besser zu lesen ist. Die Koeffizienten der Gleichungen können im Tabellenblatt geändert werden.
Wenn sie z.B. den Regler b3 =-2 einstellen, d.h. die 3 Gerade ändern zu g3: -3x+2y=-2
| | Ein LGS, zwei Gleichungen, die Geraden g1, g2 schneiden sich in G=(2,1), d.h. die Lösung des LGS (x,y)=(2,1). Neben dem geometrischen Aspekt ist die Vektorgleichung aus den Vektoren u,v aufgespannt v x+u y= b in der Ebene der x/y-Achse. Nehmen sie die 3. Gleichung g3 dazu bleibt die Lösung erhalten, weil g3 auch in G schneidet. Im 3D Fenster sehen sie die Auswirkung, weil sich durch die 3. Gleichung die Vektorgleichung in den R3 verschiebt - statt Vektoren (x,y)-Koordinaten haben wir nun Vektoren (x,y,z)-Koordinaten Die Vektoren u,v spannen eine Ebene im R3 auf. |
- dann hebt der Ergebnis Vektor b aus der Ebene der Vektorgleichung ab
- u,v können b nicht mehr abbilden
- es entstehen 3 Schnittpunkte der Geraden
- keine Lösung der LGS g1,g2,g3