Estrella de siete puntas
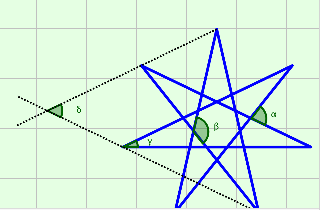
Construye la estrella de siete puntos anterior con GeoGebra
| Representa primero un heptágono regular. | 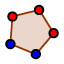 |
| Dibuja las diagonales necesarias que conforman nuestra estrella. |  ó ó  |
| Inscribe el heptágono en una circunferencia. |  , , y y  |
| Mide los ángulos que se te piden. | 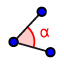 |
El ángulo interior de un polígono regular es el ángulo cóncavo que forman cualquier par consecutivo de sus lados.
En un triángulo equilátero es de . En el cuadrado, . En general si el polígono regular tiene n lados la fórmula sería .
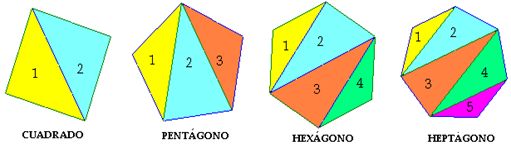
Mide el ángulo interior de nuestro heptágono regular, comprueba que se cumple la fórmula y escribe el resultado en la ventana de abajo.
Mide el ángulo interior de nuestro heptágono regular, comprueba que se cumple la fórmula y escribe el resultado en la ventana de abajo.
El ángulo central, es decir con vértice en el centro de la circunferencia, entre dos vértices consecutivos del heptágono regular es.
Obtén la medida del ángulo , cuyo vértice está por supuesto sobre la circunferencia y que abarca uno de los siete arcos y responde:
El ángulo es un ángulo interior puesto que su vértice está en el interior de la circunferencia. Su medida es:
El ángulo interior y su opuesto por el vértice, abarcan dos arcos. Teniendo en cuenta el valor de A, son:
El valor de se obtiene:
Comprueba que coincide con la medida que hiciste de . ¿Sabrías explicar porqué coincide con el ángulo interior del heptágono regular?
Mide el único ángulo exterior que hay dibujado y responde.
El ángulo es: