Funzioni invertibili e non invertibili
Proseguiamo il discorso sulle funzioni inverse, chiarendo la condizione che deve essere rispettata affinchè una funzione POSSA essere invertita: per poter invertire una funzione richiediamo che anche la sua inversa sia una funzione, ovvero definisca il risultato in modo univoco. Di conseguenza una funzione può essere invertita solo se è biunivoca, ovvero se il legame è univoco in ENTRAMBE le direzioni:
- ogni input deve dare un solo valore di output (altrimenti non è una funzione)
- dato un output, ci deve essere UN SOLO VALORE DI INPUT che lo genera (biunivocità)
![Dato che due figli (in questo caso [color=#ff0000]Miranda e Gabriel[/color]) possono avere lo stesso padre, la funzione p non è biunivoca. Ne consegue che la relazione inversa [math]p^{-1}[/math][b] NON [/b]è univoca (un padre può avere più figli, in questo caso [color=#ff0000]Josè[/color]), quindi [b]non è una funzione[/b] perché almeno uno dei suoi [i]input[/i] genera più [i]output[/i]. Ne consegue che la funzione [b]p[/b] non è invertibile. Se hai bisogno di chiarimenti sul concetto di relazione, funzione e biunivocità clicca [url=https://www.geogebra.org/m/PecCCtsR]qui[/url].](https://beta.geogebra.org/resource/bsdpn9sn/2Sviohg1ZTWvXia2/material-bsdpn9sn.png)
UN ESEMPIO DI FUNZIONE MATEMATICA NON INVERTIBILE: POTENZE (PARI) E RADICI
Anche le funzioni matematiche possono essere non biunivoche, e quindi non invertibili. Se consideriamo ad esempio la funzione , vediamo che non è biunivoca, dato due numeri opposti danno lo stesso quadrato: e , e e così via. Ne consegue che se definiamo una funzione inversa , descritta da , essa non da un risultato univoco, e quindi non è una funzione. Tradotto in termini pratici potremmo metterla così: mentre calcolando il quadrato di 8 sulla calcolatrice siamo tutti d'accordo l'unico risultato possibile è 64, calcolando la radice di 64 la calcolatrice potrebbe dare due risultati: 8 o -8. Come fa la calcolatrice a decidere quale restituire?
![L'elevamento al quadrato è una funzione - ogni numero ha [b]un solo[/b] quadrato - ma [b]non[/b] è biunivoca: lo stesso risultato è ottenuto da più valori di partenza diversi tra loro.
Ne consegue che la radice quadrata, intesa come inversa dell'elevamento al quadrato, [b]non[/b] dà un risultato univoco, e quindi [b]non[/b] è una funzione.](https://beta.geogebra.org/resource/a53n9a9f/iQ4JZ59ZRNB2E8xk/material-a53n9a9f.png)
La stessa caratteristica può essere riconosciuta osservando il grafico della funzione sul piano: per rispondere alla domanda "quale è il numero che elevato alla seconda dà 4?" nel piano cartesiano qui sotto abbiamo tracciato la linea orizzontale rossa tratteggiata, per vedere dove la curva dà come risultato . Troviamo che ci sono due per cui la parabola genera questo risultato, che ovviamente sono e e quindi quando vogliamo "tornare indietro" usando la funzione inversa ci troveremo di fronte a due alternative senza sapere quale scegliere.
Un modo per vedere graficamente che una funzione non è biunivoca è quello di tracciare una retta parallela all'asse delle , ovvero corrispondente ad un certo risultato (in questo caso : se la retta interseca la funzione in più punti, significa che ci sono più valori di input (in questo caso e ) che generano quell'output. Questo implica che la relazione inversa non sia una funzione: il suo grafico, ottenuto specchiando l'originale rispetto alla bisettrice (lo vedremo ancora più sotto), mostra chiaramente che per non si ha un risultato definito univocamente.
NOTA: Questo problema si pone non solo per la radice quadrata ma per tutte le radici pari (, perché sia che , elevate alla quarta, danno ). Le radici dispari non hanno questa ambiguità perché esse, esattamente come le potenze dispari, mantengono il segno di partenza.
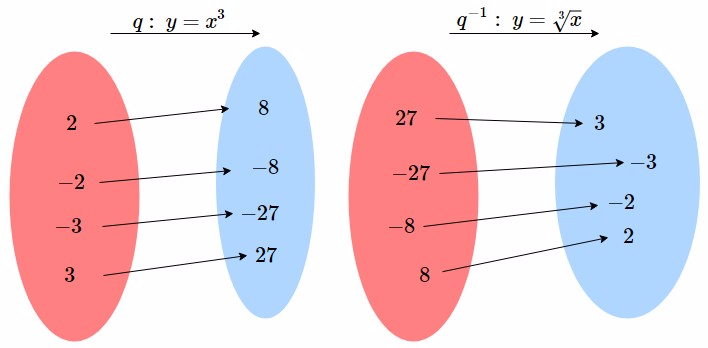
La soluzione a questo problema si ottiene ridefinendo l'operazione di radice: definiamo radice aritmetica un'operazione che, in caso di ambiguità, sceglie di considerare solo il valore positivo. Di conseguenza abbiamo che , perché tra i due possibili valori scegliamo quello positivo, mentre , perché in questo caso vi è comunque un solo risultato e quindi manteniamo quello.
Il simbolo è associato alla radice aritmetica, e quindi diventa un'operazione che restituisce un risultato univoco (e la corrispondente relazione è una funzione). L'inversa della potenza inteso in senso generale, che abbiamo usato nei primi esempi, viene chiamata radice algebrica e non ha un simbolo specifico. Nel momento in cui siamo interessati ad indicare TUTTI i numeri che elevati ad una certa potenza danno un certo valore dobbiamo dirlo esplicitamente premettendo alla radice il simbolo , come nella seguente equazione di secondo grado.
La radice in blu è la radice aritmetica, e quindi corrisponde ad un solo risultato (quello positivo, cioè 8) ma premettendo il simbolo indichiamo che sappiamo che in realtà vi sono due numeri che soddisfano l'equazione e che li vogliamo considerare entrambi.
Vediamo nell'animazione qui sotto il problema della non invertibilità delle potenze pari affrontato anche da un punto di vista grafico.
RENDERE INVERTIBILE UNA FUNZIONE RESTRINGENDO IL DOMINIO DI PARTENZA
Per rendere invertibile una funzione, si può decidere di limitare il suo insieme di partenza in modo da rendere biunivoca la funzione. Nel nostro esempio dei padri e dei figli, se modifichiamo la funzione p in questo modo la funzione diventa biunivoca, dato che ogni padre ha un solo primogenito (per i pignoli: anche nel caso dei gemelli c'è sempre uno che nasce prima dell'altro, per evidenti questioni fisico-geometriche). La funzione, quindi, restringendo l'insieme dei "figli" quello dei "primogeniti", può essere invertita.
![Se restringiamo l'insieme di partenza ai soli primogeniti, la funzione [i][b]p[/b][/i] diventa biunivoca. Riprendendo l'esempio visto prima abbiamo ipotizzato che [color=#ff0000]SOLO Miranda[/color] possa dire di essere la primogenita di Luis - quindi [color=#ff0000]Gabriel non dà più risultati perché non è il primogenito di nessuna [/color][math]\large{y}[/math][color=#ff0000]: è uscito dal dominio della funzione[/color]. La funzione ora è invertibile: anche la sua inversa genera sempre un risultato univoco e quindi è una funzione.](https://beta.geogebra.org/resource/kmwu58jg/JMHB7qMYSFMgpppW/material-kmwu58jg.png)
Anche nel caso della parabola di fatto, scegliendo di considerare il ramo "superiore" della parabola inversa, è come se avessimo limitato la funzione originale ai soli valori con .
Un altro esempio di funzioni non biunivoche che possono essere rese tali restringendo il dominio di partenza sono le funzioni goniometriche, come mostrato nell'animazione qui sotto.
Nell'animazione qui sotto puoi visualizzare il processo di inversione delle funzioni goniometriche e di alcune funzione derivate da esse.
- lo slider a ti permette di passare da una funzione all'altra
- lo slider Inversa attraversa tre fasi
- 0: Funzione originale
- 1: Evidenziazione dell'intervallo di invertibilità
- 2: Funzione inversa
IL CALCOLO DELLA FUNZIONE INVERSA
Vediamo ora una proposta di procedura per il calcolo della funzione inversa di una funzione. Tale procedura si baserà su 3 passaggi fondamentali
- Calcolo del Dominio della funzione. Se la funzione non è biunivoca, il dominio sarà la restrizione prevista per quel tipo di funzioni.
- Calcolo del Codominio (Range) corrispondente
- Inversione della funzione (ed eventuale verifica dello scambio tra Dominio e Codominio)
ESEMPIO 2
Invertiamo la funzione
1) Calcolo del Dominio, eventualmente ristretto
La funzione tangente è periodica, quindi non è biunivoca ed invertibile. Abbiamo visto che la restrizione del Dominio scelta per renderla invertibile è , imponiamo quindi che l'argomento della funzione lo rispetti: , da cui, sottraendo a tutti i termini, otteniamo che invertiremo la nostra funzione in
Il grafico di è traslato nel verso negativo delle rispetto al grafico di riferimento della tangente, quindi è logico che anche il suo Dominio di invertibilità sia traslato allo stesso modo.
2) Calcolo del Codominio corrispondente
Il codominio della tangente solitamente si estende da a (cioè la tangente assume tutti i possibili risultati). Se prendiamo questi valori estremali e li "sostituiamo" simbolicamente nella funzione otteniamo un risultato identico. Infatti se moltiplichiamo un risultato "infinitamente negativo" () per 3, otteniamo comunque un risultato infinitamente negativo, e se a questo aggiungiamo 1 il risultato sarà comunque infinitamente negativo. Simbolicamente
e allo stesso modo non cambia un risultato infinitamente positivo.
3) Inversione della funzione
Invertendo e ed isolando quest'ultima otteniamo
Entrare dei dettagli di calcolo del Dominio e del Codominio della nuova funzione sarebbe complesso (anche se fattibile); ci limitiamo quindi a dire che il suo Dominio coinciderà con il Codominio della funzione originale ed il Codominio sarà il Dominio di partenza
Per avere informazioni più precise dovremmo fare semplici considerazioni sui grafici (ma tralascia pure questa parte se sei già in difficoltà). Il grafico della funzione originale, partendo da quello mostrato sopra, ha avuto i risultati
- moltiplicati per 3, e quindi "stirati" verso le estremità come abbiamo visto accadere alla parabola
in forma base
- traslati di due unità verso l'alto.
Considerando Il grafico precedente, esso deve essere "stirato" ed "alzato" di due unità. Il punto in cui incontra l'asse delle diventa quindi da a .
Corrispondentemente potremmo notare che la funzione inversa quando azzera il contributo dall'arcotangente e quindi vale .
Nel grafico viene evidenziato questo punto , corrispondente del punto
nella funzione originale, che ci aiuta a capire le due funzioni e la loro simmetria rispetto la bisettrice dei quadranti dispari.