Funciones crecientes y decrecientes. Criterio de la primera derivada
Creciente o Decreciente
Previamente, ya habíamos visto la definición de una función creciente y decreciente.
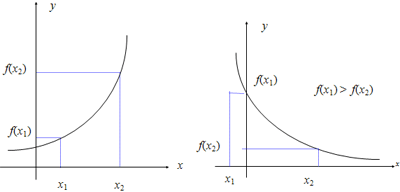
Para x2 > x1, entonces:
- Si f(x2) > f(x1) es creciente
- Si f(x2) < f(x1) es decreciente
Monotonía
Estrategia para determinar la Monotonía
- Localizar los puntos en los que f'(x) = 0 (Puntos críticos) y los puntos en los que no existe la función (revisar el denominador) para determinar los intervalos
- Toma valores de prueba entre los intervalos
- Determina el signo de f'(x) para cada valor de prueba
- Utiliza la definición de la primera derivada para determinar sí es creciente o decreciente
Criterio de la Primera Derivada
Luego de conocer los intervalos de monotonía, podemos conocer algo más: Máximos y Mínimos.
Para esto:
- Sí f'(x) va de negativa (-) a positiva (+) entonces existe un mínimo relativo
- Sí f'(x) va de positiva (+) a negativa (-) entonces existe un máximo relativo
- Sí f'(x) no cambia de signo en ambos lados entonces no es mínimo ni máximo
Criterio de la Primera Derivada
Estrategia para utilizar el Criterio de la Primera Derivada
- Localizar los puntos en los que f'(x) = 0 (Puntos críticos) y los puntos en los que no existe la función (revisar el denominador) para determinar los intervalos
- Toma valores de prueba entre los intervalos
- Determina el signo de f'(x) para cada valor de prueba
- Utiliza la definición de la primera derivada para determinar sí es creciente o decreciente
- Utiliza la definición del criterio de la primera derivada