Introducción a la Continuidad de Funciones
1. Concepto (intuitivo)
Decimos que una función es continua si su gráfica puede dibujarse de un sólo trazo, es decir, sin levantar el lápiz del papel. Las funciones polinómicas son continuas en todo
su dominio y las racionales lo son en los puntos donde no se anulan los denominadores. Por ejemplo, la siguiente gráfica
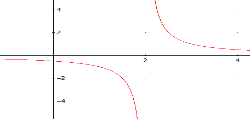
corresponde a la función
y es continua en todos los puntos excepto en , que es donde se anula el denominador.
La gráfica puede dibujarse en dos trazos.
2. Definición formal
Decimos que una función es continua en el punto si
Notemos que en el ejemplo anterior tenemos que no existe dicho límite cuando .
Decimos que la función es continua si lo es en todos los puntos.
3. Ejemplos:
Ejmplo 1: la función definida a trozos
si
si
es continua ya que en el primer intervalo (abierto) la función es polinómica y en el segundo, es la raíz cuadrada de números positivos ().
El único punto en qué puede fallar la continuidad es donde cambia la definición, es decir, en . Tenemos que comprobar si existe el límite de la función en dicho punto y coincide con el valor de la función:
como la definición de la función cambia justamente en dicho punto, tenemos que calcular los límites laterales:
Puesto que los límites laterales no coinciden, no existe el límite y, por tanto, la función no es continua en dicho punto.
La gráfica de la función es
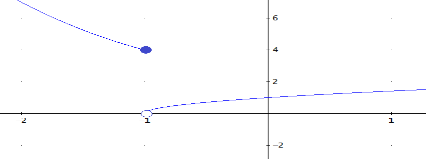
Ejemplo 2: la función tangente
no es continua en todo ya que si expresamos la función como
sabemos que no puede serlo en todos los puntos en los que se anula el denominador, que son
En los otros puntos es continua ya que es continua en todo .
La gráfica es
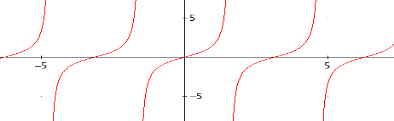
4. Otros ejemplos:
En este enlace podemos encontrar más ejemplos del estudio de la continuidad de funciones.