Stereografická obecná projekce
Promítáme středově z obecného bodu na sféře. Průmětna je kolmá na SO.
Pro určení polohy sféry vzhledem k průmětně zadáme průmět jižního pólu a okraj mapy, který je tvořen ortodromou v průmětně.
Předpokládejme, že střed promítání leží na nultém poledníku. Pak se tento zobrazí do úsečky.
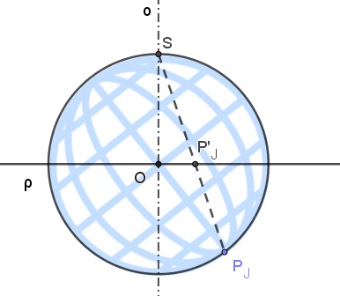
Konstrukce rovnoběžek a poledníků
1. Stereografická projekce je zadána okrajem, průmětem jižního pólu a nultého poledníku. Sestrojte rovnoběžku zeměpisné šířky a poledník zeměpisné délky.
2. Sklopíme promítací rovinu osy (Obrázek 1) a určíme průmět severního pólu PS. Sklopený střed promítání leží na obrysové kružnici, která je sklopeným nultým poledníkem.
Poledník zeměpisné délky λ
3. Zeměpisná délka se zobrazí ve skutečné velikosti, proto poledník dourčíme tečnou, která svírá s p0 orientovaný úhel λ.
4. Průmětem poledníku je kružnice určena póly a tečnou v jednom z nich.
Rovnoběžka zeměpisné šířky ϕ
5. Průmětem rovnoběžek jsou kružnice se středem na ose o. Do promítací roviny osy pravoúhle promítneme rovnoběžky (Obrázek 1) a sklopíme.
Průmět rovnoběžky určíme pomocí průsečíků A, B rovnoběžky a nultého poledníku.
6. Ve sklopení středově promítneme body [A], [B] do průmětny, tj. sestrojíme průsečíky s p0.
7. Obrazem rovnoběžky je kružnice určená průměrem AB.